헐... 건물주 체포..
소방법이 굉장히 강화되어서 이런거 점검나오면 다 체크가 되었을 건데...
건물주보다는 건물 소방관리했던 곳도 같이 처벌받을 듯 하다.
건물에 비상구등이랑 비상구 등등 체크가 지난번 의정부 화재 이후 엄청 빡세져서 허투루 할 수 없는데 이런일이 벌어지다니...
엄벌에 처할 수 밖에..
그리고 그동안 소방관들은 헬조선에서 유일한 빛들로 여겨졌는데 이번 화재 대처와 소화진압에서 보여준 아마추어같은 모습은 실로 안타까울 뿐이다.
총체적인 난국.
대한민국은 어쩌면 태어나지 않았으면 더 좋았을지 모르겠고
지도자다운 지도자 리더십의 부재가 이렇게 국가의 존망을 흔들고 있는건지 모르겠다.
2017년 12월 24일 일요일
2017년 10월 24일 화요일
2018년 정유년 띠별 운세 미리보기 1년 운세 무료운세
2018년 쥐띠운세 총정리
"자신의 실력을 너무 과신하지 마세요. 겸손하게 처신해야 허물이 없을 거에요. "
60년생 - 온고지신의 노력이 필요한 때입니다. 경험자나 윗사람의 조언을 새겨 들으세요.
72년생 - 오해를 부를 수 있는 행동은 피하세요. 자신없는 일도 피하는 것이 좋습니다.
84년생 - 성실하고 투명한 일 처리가 필요한 때입니다. 해야 할 일이 있으면 미루지 마세요.
96년생 - 다른 사람과 돈 때문에 다투지 마세요. 지나친 욕심이 화를 부를 수 있어요.
※ 2018년 소띠운세 총정리
"하늘에 구름은 가득하나 비가 내리지 않는 때입니다. 서두르거나 조급해하지 말고 때를 기다리세요."
61년생 - 다른 사람의 말은 끝까지 들어주도록 하세요. 서로의 차이를 인정하고 받아주는 것이 좋습니다.
73년생 - 자신이 가진 것을 잘 지켜야 할 때입니다. 다른 사람에게 뒤쳐지지 않도록 실력을 키우세요.
85년생 - 너무 큰 욕심 부리지 말고 작은 것에도 만족하세요. 자칫 고생만 하고 남 좋은 일만 할 수도 있습니다.
97년생 - 만사가 순조로우니 몸과 마음이 편안한 시기입니다. 다만 새로운 사람에게 쉽게 마음을 주지 마세요.
※ 2018년 범띠운세 총정리
"앞집 처녀 믿다가 장가 못 갈 수 있어요. 다른 사람에게 의지하지 말고, 직접 발로 뛰세요. "
62년생 - 아쉬움이 있어도 미련을 갖지 마세요. 맺고 끊는 것을 확실히 하는 것이 좋습니다.
74년생 - 어렵고 힘든 일은 이제 지나갔어요. 보람을 느낄 수 있는 기분 좋은 일들이 시작될 거에요.
86년생 - 주변의 뜬소문에 신경쓰지 마세요. 묵묵히 자신의 일에만 집중하는 것이 좋습니다.
98년생 - 믿는 도끼에 발등 찍힐 수 있어요. 특히 돈이 오고 가는 일은 확실히 처리하세요.
※ 2018년 토끼띠운세 총정리
"새로운 도전과 시도가 필요한 시기입니다. 평소 관심있던 취미 생활을 해보는 것도 좋아요. "
63년생 - 사사로운 정에 얽매이지 마세요. 공과 사는 확실하게 구분하는 것이 좋습니다.
75년생 - 예상하지 못한 일이 발생할 수 있어요. 당황하지 말고 융통성있게 처리하세요.
87년생 - 과유불급, 매사에 지나침을 삼가세요. 의욕이 앞서면 안 하던 실수를 할 수 있어요.
99년생 - 산토끼 쫓다가 집토끼 잃을 수 있어요. 겉치레 보다는 실속을 잘 챙기도록 하세요.
※ 2018년 용띠운세 총정리
"자신의 분수를 지키고 절제하는 것이 좋습니다. 무리한 지출이나 과음, 과식은 피하도록 하세요."
52년생 - 사람들 앞에 나서지 말고, 조용히 물러나 있으세요. 하고 싶은 말이 있어도 참는 것이 좋습니다.
64년생 - 어려운 일을 맡거나 책임이 늘어날 수 있어요. 허둥대거나 당황하지 말고 차분하게 해결해 나가세요.
76년생 - 새로운 일을 벌일 때는 자신의 능력을 잘 따져 보세요. 책임질 수 없는 일은 벌이지 않는 것이 좋습니다.
88년생 - 무엇보다 주변 인맥 관리에 힘써야 할 때입니다. 손윗사람을 잘 따르고, 아랫사람도 잘 챙기도록 하세요.
※ 2018년 뱀띠운세 총정리
"자신의 실력과 역량을 너무 과신하지 마세요. 현실적인 목표를 세우는 것이 좋습니다. "
53년생 - 작은 일로 오해가 발생할 수 있어요. 불필요한 말이나 행동은 피하도록 하세요.
65년생 - 지난 일에 대해 미련을 갖지 마세요. 한번 엎지른 물은 주워담을 수 없어요.
77년생 - 사소한 일들이 발목을 잡는 시기입니다. 작은 일에 신경쓰지 말고 대범하게 행동하세요.
89년생 - 어려운 일이 있어도 참고 버티세요. 조만간 해결의 실마리를 찾을 수 있을 거에요.
※ 2018년 말띠운세 총정리
"밝은 태양이 비추니 만사가 순조로운 시기입니다. 다만 돈을 써야 한다면 아끼지 말고 충분히 쓰세요."
54년생 - 모든 일에는 때가 있기 마련이에요. 때를 놓치면 노력이 허사가 될 수 있어요.
66년생 - 자신의 체면을 너무 앞세우지 마세요. 아랫사람의 말도 귀담아듣는 것이 좋습니다.
78년생 - 사람들에게 먼저 베풀어야 할 때입니다. 베풀 때에는 조건없이 베풀도록 하세요.
90년생 - 어려운 일이 있어도 포기하지 마세요. 손윗사람의 도움을 받으면 해결할 수 있습니다.
※ 2018년 양띠운세 총정리
"큰 욕심만 부리지 않는다면 걱정할 것이 없는 시기입니다. 새로운 사업이나 변화는 신중하게 결정하세요."
55년생 - 평소보다 내부나 집안 관리에 신경을 쓰세요. 바깥 일도 좋지만 집안 일도 신경쓰는 것이 좋습니다.
67년생 - 돌 다리도 두들겨 보고 건너는 것이 좋습니다. 자신없는 일이나 잘 모르는 일에는 뛰어들지 마세요.
79년생 - 관운이 좋으니 그동안의 노력이 빛을 발할 거에요. 다만 이동이나 여행시에는 안전을 우선하는 것이 좋습니다.
91년생 - 독단적인 행동이나 결정은 피해야 할 때입니다. 자신의 일이라도 혼자서 결정하는 것은 금물이에요.
※ 2018년 원숭이띠운세 총정리
"적극적인 행동과 노력이 필요한 때입니다. 다만 감정에 치우치지 말고 공사를 확실히 구분하세요."
56년생 - 계획만 잘 세우면 만사가 수월할 거에요. 예정에 없던 일이나 약속은 피하세요.
68년생 - 매사에 절차와 규정을 따르세요. 요령이나 편법을 쓰면 뒷감당이 어려울 수 있어요.
80년생 - 막히면 돌아가는 것이 좋습니다. 안 되는 일은 억지로 추진하지 마세요.
92년생 - 친구와 노는 것은 다음을 기약하세요. 일이나 공부에 힘쓰는 것이 좋습니다.
※ 2018년 닭띠운세 총정리
"주변의 인정을 받고, 신망을 얻을 수 있는 시기입니다. 중요한 일은 월초보다 월말에 진행하세요."
57년생 - 부하직원이나 아랫사람 때문에 마음 고생할 수 있어요. 자신의 일이 아니라면 모른 척하는 것이 좋습니다.
69년생 - 모든 문제는 쉽고 간단하게 푸는 것이 좋습니다. 너무 어렵게 생각하면 자기 꾀에 자기가 빠질 수 있어요.
81년생 - 새로운 일을 시작하려면 중순 이후에 진행하세요. 미혼이신 분들은 좋은 인연을 만날 수 있을 것입니다.
93년생 - 관운이 좋으니 취업이나 시험을 보기에 좋은 시기입니다. 여행을 떠나려면 동북쪽으로 가보세요.
※ 2018년 개띠운세 총정리
"서두르지 말고 조용히 때를 기다려야 하는 시기입니다. 마음이 급할수록 여유와 인내를 보이세요. "
58년생 - 자신의 주관을 지키도록 하세요. 주위의 유혹에 빠지면 좋은 기회를 놓칠 수 있어요.
70년생 - 겉은 화려하나 실속이 적은 시기입니다. 매사에 실속을 차리고 이득이 없는 일은 피하세요.
82년생 - 진인사대천명, 조급해하지 말고 기다리세요. 기다리던 결과는 시간이 지나야 나올 거에요.
94년생 - 윗사람의 충고를 잘 새겨들어야 할 때입니다. 어른들의 말을 들으면 자다가도 떡이 생겨요.
※ 2018년 돼지띠운세 총정리
"기다리던 소식이 찾아오거나 소원이 이루어지는 시기입니다. 다만 가족이나 가까운 사람들과의 갈등에 유의하세요."
59년생 - 지나간 일은 다시 들추지 말고 묻어두도록 하세요. 과거보다는 현재와 미래를 우선해야 합니다.
71년생 - 일이나 사업의 확장을 꾀해도 좋은 시기입니다. 다만 주변에서 반대하는 일은 무리하게 추진하지 마세요.
83년생 - 할 일도 많고 신경쓸 것도 많으니 심신이 피곤할 수 있어요. 틈틈이 쉬면서 스트레스를 푸는 것이 좋습니다.
95년생 - 새로운 친구나 마음에 드는 이성을 만나는 시기입니다. 다만 노는 것도 좋지만 해야 할 일을 소홀히 하지 마세요.
"자신의 실력을 너무 과신하지 마세요. 겸손하게 처신해야 허물이 없을 거에요. "
60년생 - 온고지신의 노력이 필요한 때입니다. 경험자나 윗사람의 조언을 새겨 들으세요.
72년생 - 오해를 부를 수 있는 행동은 피하세요. 자신없는 일도 피하는 것이 좋습니다.
84년생 - 성실하고 투명한 일 처리가 필요한 때입니다. 해야 할 일이 있으면 미루지 마세요.
96년생 - 다른 사람과 돈 때문에 다투지 마세요. 지나친 욕심이 화를 부를 수 있어요.
※ 2018년 소띠운세 총정리
"하늘에 구름은 가득하나 비가 내리지 않는 때입니다. 서두르거나 조급해하지 말고 때를 기다리세요."
61년생 - 다른 사람의 말은 끝까지 들어주도록 하세요. 서로의 차이를 인정하고 받아주는 것이 좋습니다.
73년생 - 자신이 가진 것을 잘 지켜야 할 때입니다. 다른 사람에게 뒤쳐지지 않도록 실력을 키우세요.
85년생 - 너무 큰 욕심 부리지 말고 작은 것에도 만족하세요. 자칫 고생만 하고 남 좋은 일만 할 수도 있습니다.
97년생 - 만사가 순조로우니 몸과 마음이 편안한 시기입니다. 다만 새로운 사람에게 쉽게 마음을 주지 마세요.
※ 2018년 범띠운세 총정리
"앞집 처녀 믿다가 장가 못 갈 수 있어요. 다른 사람에게 의지하지 말고, 직접 발로 뛰세요. "
62년생 - 아쉬움이 있어도 미련을 갖지 마세요. 맺고 끊는 것을 확실히 하는 것이 좋습니다.
74년생 - 어렵고 힘든 일은 이제 지나갔어요. 보람을 느낄 수 있는 기분 좋은 일들이 시작될 거에요.
86년생 - 주변의 뜬소문에 신경쓰지 마세요. 묵묵히 자신의 일에만 집중하는 것이 좋습니다.
98년생 - 믿는 도끼에 발등 찍힐 수 있어요. 특히 돈이 오고 가는 일은 확실히 처리하세요.
※ 2018년 토끼띠운세 총정리
"새로운 도전과 시도가 필요한 시기입니다. 평소 관심있던 취미 생활을 해보는 것도 좋아요. "
63년생 - 사사로운 정에 얽매이지 마세요. 공과 사는 확실하게 구분하는 것이 좋습니다.
75년생 - 예상하지 못한 일이 발생할 수 있어요. 당황하지 말고 융통성있게 처리하세요.
87년생 - 과유불급, 매사에 지나침을 삼가세요. 의욕이 앞서면 안 하던 실수를 할 수 있어요.
99년생 - 산토끼 쫓다가 집토끼 잃을 수 있어요. 겉치레 보다는 실속을 잘 챙기도록 하세요.
※ 2018년 용띠운세 총정리
"자신의 분수를 지키고 절제하는 것이 좋습니다. 무리한 지출이나 과음, 과식은 피하도록 하세요."
52년생 - 사람들 앞에 나서지 말고, 조용히 물러나 있으세요. 하고 싶은 말이 있어도 참는 것이 좋습니다.
64년생 - 어려운 일을 맡거나 책임이 늘어날 수 있어요. 허둥대거나 당황하지 말고 차분하게 해결해 나가세요.
76년생 - 새로운 일을 벌일 때는 자신의 능력을 잘 따져 보세요. 책임질 수 없는 일은 벌이지 않는 것이 좋습니다.
88년생 - 무엇보다 주변 인맥 관리에 힘써야 할 때입니다. 손윗사람을 잘 따르고, 아랫사람도 잘 챙기도록 하세요.
※ 2018년 뱀띠운세 총정리
"자신의 실력과 역량을 너무 과신하지 마세요. 현실적인 목표를 세우는 것이 좋습니다. "
53년생 - 작은 일로 오해가 발생할 수 있어요. 불필요한 말이나 행동은 피하도록 하세요.
65년생 - 지난 일에 대해 미련을 갖지 마세요. 한번 엎지른 물은 주워담을 수 없어요.
77년생 - 사소한 일들이 발목을 잡는 시기입니다. 작은 일에 신경쓰지 말고 대범하게 행동하세요.
89년생 - 어려운 일이 있어도 참고 버티세요. 조만간 해결의 실마리를 찾을 수 있을 거에요.
※ 2018년 말띠운세 총정리
"밝은 태양이 비추니 만사가 순조로운 시기입니다. 다만 돈을 써야 한다면 아끼지 말고 충분히 쓰세요."
54년생 - 모든 일에는 때가 있기 마련이에요. 때를 놓치면 노력이 허사가 될 수 있어요.
66년생 - 자신의 체면을 너무 앞세우지 마세요. 아랫사람의 말도 귀담아듣는 것이 좋습니다.
78년생 - 사람들에게 먼저 베풀어야 할 때입니다. 베풀 때에는 조건없이 베풀도록 하세요.
90년생 - 어려운 일이 있어도 포기하지 마세요. 손윗사람의 도움을 받으면 해결할 수 있습니다.
※ 2018년 양띠운세 총정리
"큰 욕심만 부리지 않는다면 걱정할 것이 없는 시기입니다. 새로운 사업이나 변화는 신중하게 결정하세요."
55년생 - 평소보다 내부나 집안 관리에 신경을 쓰세요. 바깥 일도 좋지만 집안 일도 신경쓰는 것이 좋습니다.
67년생 - 돌 다리도 두들겨 보고 건너는 것이 좋습니다. 자신없는 일이나 잘 모르는 일에는 뛰어들지 마세요.
79년생 - 관운이 좋으니 그동안의 노력이 빛을 발할 거에요. 다만 이동이나 여행시에는 안전을 우선하는 것이 좋습니다.
91년생 - 독단적인 행동이나 결정은 피해야 할 때입니다. 자신의 일이라도 혼자서 결정하는 것은 금물이에요.
※ 2018년 원숭이띠운세 총정리
"적극적인 행동과 노력이 필요한 때입니다. 다만 감정에 치우치지 말고 공사를 확실히 구분하세요."
56년생 - 계획만 잘 세우면 만사가 수월할 거에요. 예정에 없던 일이나 약속은 피하세요.
68년생 - 매사에 절차와 규정을 따르세요. 요령이나 편법을 쓰면 뒷감당이 어려울 수 있어요.
80년생 - 막히면 돌아가는 것이 좋습니다. 안 되는 일은 억지로 추진하지 마세요.
92년생 - 친구와 노는 것은 다음을 기약하세요. 일이나 공부에 힘쓰는 것이 좋습니다.
※ 2018년 닭띠운세 총정리
"주변의 인정을 받고, 신망을 얻을 수 있는 시기입니다. 중요한 일은 월초보다 월말에 진행하세요."
57년생 - 부하직원이나 아랫사람 때문에 마음 고생할 수 있어요. 자신의 일이 아니라면 모른 척하는 것이 좋습니다.
69년생 - 모든 문제는 쉽고 간단하게 푸는 것이 좋습니다. 너무 어렵게 생각하면 자기 꾀에 자기가 빠질 수 있어요.
81년생 - 새로운 일을 시작하려면 중순 이후에 진행하세요. 미혼이신 분들은 좋은 인연을 만날 수 있을 것입니다.
93년생 - 관운이 좋으니 취업이나 시험을 보기에 좋은 시기입니다. 여행을 떠나려면 동북쪽으로 가보세요.
※ 2018년 개띠운세 총정리
"서두르지 말고 조용히 때를 기다려야 하는 시기입니다. 마음이 급할수록 여유와 인내를 보이세요. "
58년생 - 자신의 주관을 지키도록 하세요. 주위의 유혹에 빠지면 좋은 기회를 놓칠 수 있어요.
70년생 - 겉은 화려하나 실속이 적은 시기입니다. 매사에 실속을 차리고 이득이 없는 일은 피하세요.
82년생 - 진인사대천명, 조급해하지 말고 기다리세요. 기다리던 결과는 시간이 지나야 나올 거에요.
94년생 - 윗사람의 충고를 잘 새겨들어야 할 때입니다. 어른들의 말을 들으면 자다가도 떡이 생겨요.
※ 2018년 돼지띠운세 총정리
"기다리던 소식이 찾아오거나 소원이 이루어지는 시기입니다. 다만 가족이나 가까운 사람들과의 갈등에 유의하세요."
59년생 - 지나간 일은 다시 들추지 말고 묻어두도록 하세요. 과거보다는 현재와 미래를 우선해야 합니다.
71년생 - 일이나 사업의 확장을 꾀해도 좋은 시기입니다. 다만 주변에서 반대하는 일은 무리하게 추진하지 마세요.
83년생 - 할 일도 많고 신경쓸 것도 많으니 심신이 피곤할 수 있어요. 틈틈이 쉬면서 스트레스를 푸는 것이 좋습니다.
95년생 - 새로운 친구나 마음에 드는 이성을 만나는 시기입니다. 다만 노는 것도 좋지만 해야 할 일을 소홀히 하지 마세요.
2017년 10월 18일 수요일
노가다 평균 수명. Average life expectancy
미국은 bureau of labor statistics 라는 노동부의 하위 부서에서 통계를 내놨더라.
한국과 미국은 근무조건이 다르겠지만 궁금해서 한번 봤다.
일단 모든 직업 전체 평균은 78살 조금 넘더라
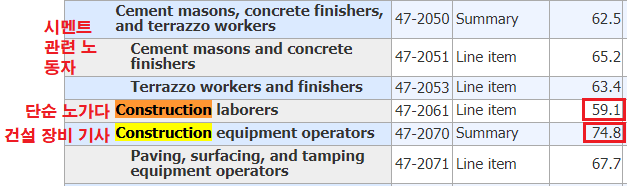
그냥 건설 현장 단순 노가다를 봤음
시멘트로 공구리 치는 애들은 평균수명이 62 ~ 65 살정도 됨. 맨날 시멘트 가루 마셔서 그런듯
단순 건설 노가다는 존나 심각함. 59살 밖에 못삶.
그나마 중장비 다루는 애들은 75살로 평균이랑 비슷하게 살더라.
용접은 시발 그냥 앵간하면 용접 하지마라.
용접공 평균 수명 53.4살이다.
용접이 본인이 느끼는거랑 상관없이 얼마나 몸에 부담이 가는 직업인지 알수있는 부분
참고로 지디게이 39살이라던데. 당장 결혼해봤자 앞으로 15년밖에 더 못사니까 앵간하면 그냥 결혼하지마라.
트럭 운전은 꽤나 준수함. 74세.
근데 고중량 트럭이나 트레일러 끄는 애들은 평균 수명이 65살 밖에 안됨.
미국은 일주일 내내 달려야되니까 저런걸수도 있다. 아무튼 상대적으로 다른 노가다보다는 안전함.
노가다 게이들. 특히 용접이랑 시멘트 공구리, 막노동들아.
건강챙기면서 일해라.
우리집은 자산기준 상위 몇% ?
[선 세 줄 요약]
- 가구 순자산 보유액 30억원= 대한민국 상위 0.58%
- 가구 순자산 보유액 23억원= 대한민국 상위 1%
- 가구 순자산 보유액 10억원= 대한민국 상위 4.5%
자료 출처: 금감원 보도자료(2016년 가계금융,복지 조사결과)
1. 순자산이란 부채와 같은 타인자본을 제외한 자산 즉, 자기자본을 의미한다
순자산을 보유액 구간별로 보면, 1억원 미만 보유가구(34.8%), 1~2억원(19.2%), 2~3억원(14.0%) 순으로, 3억 미만 가구가 전체의 68.0%를 차지하며, 10억원 이상은 4.5%를 차지하고 있다.
즉, 가구 순자산 10억을 달성하면 대한민국 상위 4.5%라는 의미다. (중요한 점은 단위가 명이 아닌 가구라는 것)
부동산 가격은 공시지가가 아닌 실거래가를 토대로한 시가로 산정하였으므로 상당히 신빙성 높은 자료라고 할 수 있음
한국에서 나오는 그 어떠한 자료 보다도 정확도가 높다
자료출처: KB국민은행
2. 서울시 평균 아파트 매매가가 6억 170만원(2017년 기준)
저 가격대의 아파트를 융자 없이 자가로 보유하고 있으면 대한민국 상위 10%라고 할 수 있다.
하지만 서울시를 기준으로 봤을 때 거주하고 있는 주택, 아파트의 자가주택보유율(자가점유비율)은 약 42.1% 수준 [출처: 나라지표]
즉, 나머지 57.9%는 남의 집에서 살고 있다는 의미다
자가로 보유한 42.1%도 융자 없이 보유한 세대는 일부
감기 빨리 낫는 물리학적 방법
감기는 바이러스 감염이야
주로 코점막이나 비인두에 바이러스가 침입해 콧물나고 목이 따갑게 되잖아
감기가 왔다 싶으면 어떻게 하면 가장 좋을까?
이 문제는 개인의 건강문제를 넘어 개인의 경제적가치, 사회적 생산성향상 차원에서 바라봐야 된다고 생각하거든
감기의 이환기간을 하루 이틀이라도 줄일 수 있으면 전세계적으로 어마어마한 경제적 가치와 생산성 향상을 도모할 수 있을거라는거지
감기에 잘 걸리지 않는 예방적 방법은 평소 건강을 잘 유지하는거야 비타민C니 아연이니 에키네시아니 개소리 믿지 말고 평소에 운동하고 건강한 음식먹어라
그럼 감기에 걸릴랑 말랑 하는 것 같다 - 뜨거운 국이나 스프를 먹어, 바이러스 새끼들이 더 설레발 치기 전에 40도 이상 뜨거운 국물과 건데기를 아구아구 삼키면서 구강 비인두 코점막의 바이러스를 아작내버려
그럼 감기가 도지기 시작해서 몸살과 머리가 지끈거리기 시작했어 열도 조금 나는 것 같다 - 이불 꽁꽁 싸매고 누워라, 욕탕에 뜨거운 물받아 놓고 누워라 왜냐하면 눕는다는건 너의 육신이 중력의 스트레스에 벗어나 혈중 코티졸 농도를 떨어트려 바이러스와 한창 싸우고 있는 니 면역력에 조금이라도 더 힘을 줄 수 있기 때문이야
그럼 계속 쳐 누워있으면 낫느냐? 면역력이 바이러스를 좀 누르기 시작하여 통증이 좀 가시면 몸을 움직여줘야 해 왜냐하면 오래 누워있으면 그 자체가 스트레스로 작용하기 시작하기 떄문이야 그래서 스트레칭과 적당한 유산소운동(웨이트트레이닝은 자제하고)을 해주면 엔돌핀이 분비되기 때문에 스트레스를 완화하고 면역력을 적극적으로 부스팅할 수 있거든, 이게 우리가 타이레놀을 사용하는 이유야, 타이레놀은 트라마돌과 마찬가지로 일종의 오피오이드(아편)수용체에 작용하기 때문에 일시적으로 통증을 줄여서 감염에 대한 면역력을 보조해 주는 작용을 할 수 있는거야, 예전에 노인들이 아편이 마약으로 지정되기 전에 집에 아편을 상비해 두고 만병통치약 마냥 사용했던 것도 이런 메카니즘이 있어, 근데 문제는 타이레놀도 그렇고 트라마돌도 그렇고 아파서 먹을때는 금방 통증이 해소되니까 딱 좋은데 이게 약발 떨어지면(대략 하루뒤) 리바운드로 강력한 두통이나 구역구토가 발생할 수 있다는거지, 근데 운동으로 얻는 내생적인 오피오이드(엔돌핀 등)은 그런 리바운드 없이 니 컨디션과 기분, 면역력을 끌어올려주는거지
2줄요약) 감기의 물리학적 치료
1. 40도 이상 열로 조진다
2. 중력 스트레스에서 벗어난다, 그 다음에는 가벼운 운동해라
주로 코점막이나 비인두에 바이러스가 침입해 콧물나고 목이 따갑게 되잖아
감기가 왔다 싶으면 어떻게 하면 가장 좋을까?
이 문제는 개인의 건강문제를 넘어 개인의 경제적가치, 사회적 생산성향상 차원에서 바라봐야 된다고 생각하거든
감기의 이환기간을 하루 이틀이라도 줄일 수 있으면 전세계적으로 어마어마한 경제적 가치와 생산성 향상을 도모할 수 있을거라는거지
감기에 잘 걸리지 않는 예방적 방법은 평소 건강을 잘 유지하는거야 비타민C니 아연이니 에키네시아니 개소리 믿지 말고 평소에 운동하고 건강한 음식먹어라
그럼 감기에 걸릴랑 말랑 하는 것 같다 - 뜨거운 국이나 스프를 먹어, 바이러스 새끼들이 더 설레발 치기 전에 40도 이상 뜨거운 국물과 건데기를 아구아구 삼키면서 구강 비인두 코점막의 바이러스를 아작내버려
그럼 감기가 도지기 시작해서 몸살과 머리가 지끈거리기 시작했어 열도 조금 나는 것 같다 - 이불 꽁꽁 싸매고 누워라, 욕탕에 뜨거운 물받아 놓고 누워라 왜냐하면 눕는다는건 너의 육신이 중력의 스트레스에 벗어나 혈중 코티졸 농도를 떨어트려 바이러스와 한창 싸우고 있는 니 면역력에 조금이라도 더 힘을 줄 수 있기 때문이야
그럼 계속 쳐 누워있으면 낫느냐? 면역력이 바이러스를 좀 누르기 시작하여 통증이 좀 가시면 몸을 움직여줘야 해 왜냐하면 오래 누워있으면 그 자체가 스트레스로 작용하기 시작하기 떄문이야 그래서 스트레칭과 적당한 유산소운동(웨이트트레이닝은 자제하고)을 해주면 엔돌핀이 분비되기 때문에 스트레스를 완화하고 면역력을 적극적으로 부스팅할 수 있거든, 이게 우리가 타이레놀을 사용하는 이유야, 타이레놀은 트라마돌과 마찬가지로 일종의 오피오이드(아편)수용체에 작용하기 때문에 일시적으로 통증을 줄여서 감염에 대한 면역력을 보조해 주는 작용을 할 수 있는거야, 예전에 노인들이 아편이 마약으로 지정되기 전에 집에 아편을 상비해 두고 만병통치약 마냥 사용했던 것도 이런 메카니즘이 있어, 근데 문제는 타이레놀도 그렇고 트라마돌도 그렇고 아파서 먹을때는 금방 통증이 해소되니까 딱 좋은데 이게 약발 떨어지면(대략 하루뒤) 리바운드로 강력한 두통이나 구역구토가 발생할 수 있다는거지, 근데 운동으로 얻는 내생적인 오피오이드(엔돌핀 등)은 그런 리바운드 없이 니 컨디션과 기분, 면역력을 끌어올려주는거지
2줄요약) 감기의 물리학적 치료
1. 40도 이상 열로 조진다
2. 중력 스트레스에서 벗어난다, 그 다음에는 가벼운 운동해라
현세대 최고의 수학자 테렌스 타오 (Terence Tao
陶哲軒, Terence Tao
1975년 7월 17일 호주 에서 태어난 중국인 아빠와 홍콩인 엄마사이에서 태어난 동양계 오스트레일리아-미국인.
9살에 대학과정의 이공계 수업을 들었으며, 존스 홉킨스의 Study of Exceptional Talent(영재수업 프로그램)에서 최고의 성적을 거두었으며 9살에 수학영역 800만점에 760점을 받는다.
main-qimg-83f7722a245a2cef737ac6e9ff700ab5-c.jpeg
이후 국제수학올림피아드에서 1986, 1987, 1988년에 각각 동상, 은상, 금상을 차례로 최연소의 나이로 수상한다.
14살의 나이에 MIT 과학연구기관에서 일했으며, 15살에 최초로 보조 논문을 낸다. 16살에 학사와 석사를 동시에 플린더스 대학교의 교수밑에서 받고, 세계에서 가장 영예로운 장학금 중 하나인 풀브라이트 장학금을 받고 프린스턴 대학교의 박사과정을 밟는다.
이후 21살의 나이에 프린스턴 대학교에서 박사학위를 받고, 24살에 미국 남서부 캘리포니아의 UCLA에서 정교수로 취임하며 UCLA 역사상 최연소의 천재교수로 기록을 남긴다. 참고로 현존하는 가장 지능이 높은 사람으로 알려져있다. (IQ 237이라고 알려졌었다)
Terence_Tao.jpg
(20살 프린스턴 대학교 박사과정 당시)
이후 옥스포드 대학의 Ben J. Green과 함께 그린-타오 정리(Green-Tao therom)를 발표한다.
이는 정수론에서 소수의 대수적 수열에 관한 천재적 정리로, 소수의 수열이 임의의 등차수열을 포함한다는 수백년간 풀리지 않아온 쌍둥이 소수 가설에 대한 간접적 알고리즘을 제시하는 정리이다.
이 공로로 타오는 오스트레일리아 수학자 협회 메달(2004) 을 받는다
그리고 정수론 뿐만 아니라 해석학, 미분기하, 위상수학, 순열조합분석론 등의 한계가 없는 방대한 분야에서 수많은 정리와 논문을 씀으로써, 마침내 2006년 스페인 마드리드에서 수학자로서 최고의 명예인 필즈상(Fields medal)을 수여한다.
저명한 과학 학술지인 "New Scientist"에서는 수학의 분야에 한계가 없이 천재적인 업적을 이루고있는 테렌스 타오에 대해서 이렇게 밝혔다
"Such is Tao's reputation that mathematicians now compete to interest him in their problems, and he is becoming a kind of Mr Fix-it for frustrated researchers. "If you're stuck on a problem, then one way out is to interest Terence Tao," says Charles Fefferman [professor of mathematics at Princeton University]."
"이런 타오의 업적들은 현재 수많은 수학자들은 타오를 그들의 영역에 관심이 생기게 하기 위해서 온갖 노력을 하게만들고있다, (단순 천재가 아니라) 혼돈에 빠진 연구자들에게 타오는 무엇이든지 정리를 내고 뚝딱 고쳐주는 정도이다. "만약 어떠한 문제에 봉착했다면, 이를 해결할 수 있는 한 가지 방법은 이 문제로 타오의 관심을 끄는 것이다 (오로지 그만이 해결가능하다)" - Charles Fefferman 프린스턴 대학의 수학과 교수-
1464575726877.jpg
테렌스 타오의 가족 (아내와 자식들)
마침내 2007년 오스트레일리아를 빛낸 인물 1위에 등극했으며, 오스트레일리아 과학 아카데미(Austrailian Academy of Science)의 일원이 되었고, 영국 런던의 황립협회(Royal Society)의 일원으로 추대받았다. 이 해에, 타오는 무려 슈메레디 정규성 보조 정리( )를 확장하여 정리한 "타오 부등식"(Tao Inequality)을 발표한다.
(https://www.math.uni-bielefeld.de/ahlswede/homepage/public/217.pdf) 슈메레디 정규성 보조 정리를 확장한 "타오 부등식" 논문
terry-edp.png
타오의 주요 연구분야는 상당히 고차원적인 수학으로, 그 분야의 교수조차도 끊임없는 연구가 없다면 이해할 수 없는 수학이다, 더구나 그의 연구분야의 범위가 상당히 방대한 것도 테렌스 타오를 "프린스턴의 외계인"으로 불리게 만든 이유다.
2008_tao_waterman.jpg
필즈상을 수상하는 테렌스 타오
현재까지 무려 250편의 논문을 발표했고 (절반 정도는 난제에 관한 증명이다, 즉 100개이상의 현존하는 난제를 겨우 수학자 인생 20년동안 모두 해결했다), 17권의 도서를 출간했다. 그가 지금껏 받은 국제 명예의 상은 다음과 같다.
살렘 (Salem) 상 (2000) 보셰 기념상 (2002) Clay Research Award (2003) 호주 수학 협회 메달 (2005) 오스트 로프 스키 상 (2005) ISAAC 상 (38) (2005) Levi L. Conant Prize (2005) 필즈상 (2006) 맥아더 상 (2006) SASTRA Ramanujan Prize (2006) 슬로안 펠로우쉽 (2006) Alan T. Waterman Award (2008) 왕립 학회 연구원 (2007) 온 세미 메달 (2008) 파이살 국제상 (2010) 미국 예술 과학 아카데미 입학 (2009) Nemmers 수학 부문 (2010) 폴리 마상 (2010) Crafoord Prize (2012) Simons Investigator (2012) 교육 우수상 센터 (Joseph I. Lieberman Award(2013) 창립 수령자) 수학 분야의 획기적인 상 (2014 년, 2014 년 수상) 로얄 메달 (2014) PROSE 상 (2015 년) 존스 홉킨스 CTY Distinguished Alumnus(2014)
현재 그의 나이 겨우 42살이다. 프린스턴 대학교의 수학 연구소와 하버드의 클레이연구소에서는 "19세기에 가우스, 20세기에 노이만이 존재했다면, 21세기에는 테렌스 타오가 있다" 라는 말로 현존하는 최고의 수학자라는 수식어를 대신한다.
1975년 7월 17일 호주 에서 태어난 중국인 아빠와 홍콩인 엄마사이에서 태어난 동양계 오스트레일리아-미국인.
9살에 대학과정의 이공계 수업을 들었으며, 존스 홉킨스의 Study of Exceptional Talent(영재수업 프로그램)에서 최고의 성적을 거두었으며 9살에 수학영역 800만점에 760점을 받는다.
main-qimg-83f7722a245a2cef737ac6e9ff700ab5-c.jpeg
이후 국제수학올림피아드에서 1986, 1987, 1988년에 각각 동상, 은상, 금상을 차례로 최연소의 나이로 수상한다.
14살의 나이에 MIT 과학연구기관에서 일했으며, 15살에 최초로 보조 논문을 낸다. 16살에 학사와 석사를 동시에 플린더스 대학교의 교수밑에서 받고, 세계에서 가장 영예로운 장학금 중 하나인 풀브라이트 장학금을 받고 프린스턴 대학교의 박사과정을 밟는다.
이후 21살의 나이에 프린스턴 대학교에서 박사학위를 받고, 24살에 미국 남서부 캘리포니아의 UCLA에서 정교수로 취임하며 UCLA 역사상 최연소의 천재교수로 기록을 남긴다. 참고로 현존하는 가장 지능이 높은 사람으로 알려져있다. (IQ 237이라고 알려졌었다)
Terence_Tao.jpg
(20살 프린스턴 대학교 박사과정 당시)
이후 옥스포드 대학의 Ben J. Green과 함께 그린-타오 정리(Green-Tao therom)를 발표한다.
이는 정수론에서 소수의 대수적 수열에 관한 천재적 정리로, 소수의 수열이 임의의 등차수열을 포함한다는 수백년간 풀리지 않아온 쌍둥이 소수 가설에 대한 간접적 알고리즘을 제시하는 정리이다.
이 공로로 타오는 오스트레일리아 수학자 협회 메달(2004) 을 받는다
그리고 정수론 뿐만 아니라 해석학, 미분기하, 위상수학, 순열조합분석론 등의 한계가 없는 방대한 분야에서 수많은 정리와 논문을 씀으로써, 마침내 2006년 스페인 마드리드에서 수학자로서 최고의 명예인 필즈상(Fields medal)을 수여한다.
저명한 과학 학술지인 "New Scientist"에서는 수학의 분야에 한계가 없이 천재적인 업적을 이루고있는 테렌스 타오에 대해서 이렇게 밝혔다
"Such is Tao's reputation that mathematicians now compete to interest him in their problems, and he is becoming a kind of Mr Fix-it for frustrated researchers. "If you're stuck on a problem, then one way out is to interest Terence Tao," says Charles Fefferman [professor of mathematics at Princeton University]."
"이런 타오의 업적들은 현재 수많은 수학자들은 타오를 그들의 영역에 관심이 생기게 하기 위해서 온갖 노력을 하게만들고있다, (단순 천재가 아니라) 혼돈에 빠진 연구자들에게 타오는 무엇이든지 정리를 내고 뚝딱 고쳐주는 정도이다. "만약 어떠한 문제에 봉착했다면, 이를 해결할 수 있는 한 가지 방법은 이 문제로 타오의 관심을 끄는 것이다 (오로지 그만이 해결가능하다)" - Charles Fefferman 프린스턴 대학의 수학과 교수-
1464575726877.jpg
테렌스 타오의 가족 (아내와 자식들)
마침내 2007년 오스트레일리아를 빛낸 인물 1위에 등극했으며, 오스트레일리아 과학 아카데미(Austrailian Academy of Science)의 일원이 되었고, 영국 런던의 황립협회(Royal Society)의 일원으로 추대받았다. 이 해에, 타오는 무려 슈메레디 정규성 보조 정리( )를 확장하여 정리한 "타오 부등식"(Tao Inequality)을 발표한다.
(https://www.math.uni-bielefeld.de/ahlswede/homepage/public/217.pdf) 슈메레디 정규성 보조 정리를 확장한 "타오 부등식" 논문
terry-edp.png
타오의 주요 연구분야는 상당히 고차원적인 수학으로, 그 분야의 교수조차도 끊임없는 연구가 없다면 이해할 수 없는 수학이다, 더구나 그의 연구분야의 범위가 상당히 방대한 것도 테렌스 타오를 "프린스턴의 외계인"으로 불리게 만든 이유다.
2008_tao_waterman.jpg
필즈상을 수상하는 테렌스 타오
현재까지 무려 250편의 논문을 발표했고 (절반 정도는 난제에 관한 증명이다, 즉 100개이상의 현존하는 난제를 겨우 수학자 인생 20년동안 모두 해결했다), 17권의 도서를 출간했다. 그가 지금껏 받은 국제 명예의 상은 다음과 같다.
살렘 (Salem) 상 (2000) 보셰 기념상 (2002) Clay Research Award (2003) 호주 수학 협회 메달 (2005) 오스트 로프 스키 상 (2005) ISAAC 상 (38) (2005) Levi L. Conant Prize (2005) 필즈상 (2006) 맥아더 상 (2006) SASTRA Ramanujan Prize (2006) 슬로안 펠로우쉽 (2006) Alan T. Waterman Award (2008) 왕립 학회 연구원 (2007) 온 세미 메달 (2008) 파이살 국제상 (2010) 미국 예술 과학 아카데미 입학 (2009) Nemmers 수학 부문 (2010) 폴리 마상 (2010) Crafoord Prize (2012) Simons Investigator (2012) 교육 우수상 센터 (Joseph I. Lieberman Award(2013) 창립 수령자) 수학 분야의 획기적인 상 (2014 년, 2014 년 수상) 로얄 메달 (2014) PROSE 상 (2015 년) 존스 홉킨스 CTY Distinguished Alumnus(2014)
현재 그의 나이 겨우 42살이다. 프린스턴 대학교의 수학 연구소와 하버드의 클레이연구소에서는 "19세기에 가우스, 20세기에 노이만이 존재했다면, 21세기에는 테렌스 타오가 있다" 라는 말로 현존하는 최고의 수학자라는 수식어를 대신한다.
모래더미의 역설 (Sand-pile paradox)
사막의 풍경은 아주 적막하지만, 사막만이 가지는 모래들의 고요한 아름다움을 간직하고 있다.
무수히 많은 모래들이 이루는 고요함과 더불어 사막에서만 찾아볼 수 있는 진귀한 풍경들도 많다. 특히, 미국 동,남부~중부에 걸쳐있는 광활한 Desert valley의 모래들은 상당히 부드럽고 입자가 무척작다.
그럼 여기서 모래더미를 잠깐 살펴보자.
487610394.jpg
어릴때 늘 모래를 가지고 놀았듯이, 우리는 위의 "모래더미"에서 모래알 하나씩을 뺴내고 그릇에 옮기는 놀이를 해보기로 하자.
우리는 모래알 한알을 빼내어 그릇에 옮겨놓았다.
이 모래알 한알이 빠진 "모래더미"는 여전히 "모래더미"이다.
이번엔 두번째, 세번째 시도를 해보자.
...
몇알이 빠졌던 상관없이 "모래더미"는 여전히 건재하다. 왜냐하면 몇알이 빠졌던 상관없이 "모래더미"는 여전히 모래더미이기 때문이다.
그런데 셀수없이 많은 시도를 해보자면 모래더미는 결국 모래알 한알만 남게될 것이다.
그러나 앞선 논리에 따르자면 이 모래알 한알만 남은 모래더미 "조차도" 훌륭한 [모래더미]가 된다.
depositphotos_11060156-stock-photo-3d-white-leaning-back-against.jpg
뭔가 이상하다. 분명 우리는 한번, 두번, 세번 ... 시도를 해도 눈앞에 모래더미가 여전히 남아있다는 사실을 이해할 수 있다.
그러나 계속 시도를 하게되면 남아있는 그 "모래더미"는 결국 "모래더미"가 아니게 된다.
우리는 상황이 조금더 복잡하고 심각해진다는것을 예감할 수 있다.
조금더 수학적, 논리적으로 접근을 해보자.
1. 모래더미는 모래들의 집합이다
2. 모래더미에서 n개 정도의 모래알을 덜어낸다고 해서 기존의 모래더미와의 차이가 크지 않으므로, n+1개의 모래알을 덜어내도 여전히 모래더미이다.
3. 1) 2)의 논리와 수학적 귀납법 (Mathematical Induction)을 이용하면 모래를 모두 덜어내어도 여전히 모래더미이다.
220px-Tannin_heap.jpeg
아니다. 우리는 2번까지는 고개를 끄덕이며 동의하지만, 3번의 논리에는 고개를 완강히 저으며 "당연히 아니다" 라고 말할 수 있다.
그러나 1,2,3번의 논리에는 어떠한 논리적 오류도 존재하지 않는다.
여기서 수학적 귀납법이 뭘까? 다음과 같은 연역법(Deductive reasoning)의 한 방법이다.
51-induction-5-638.jpg
1. 어떠한 Proposition (명제) P(n)에 관해서 P(1) 혹은 P(0)과 같은 "자명한" 경우에 명제가 성립함을 밝힌다
2. P(n)이 P(k)일때 성립한다고 가정한뒤, P(n) = P(k+1)임을 증명한다.
3. k=1일때 P(n)이 성립한다면, P(k+1)일때도 성립해야하므로, P(2)일때도 성립, 이를 반복, k에 대하여 P(n)이 무한히 성립한다.
조금더 쉽게 풀어쓰자면
1. 첫번째 도미노가 쓰러지는지 확인한다
2. n번째 도미노가 쓰러지면 n+1 번째 도미노도 쓰러진다는 것을 확인한다
3. 결국 모든 도미노는 무사히 쓰러진다
결국 수학적 귀납법에 의해서 명제 P(n) = "n개의 모래알을 뺀 모래더미는 여전히 모래더미다" 의 도미노는 모두 무사히 쓰러져야"한다".
그런데, 우리는 그렇지 않다는것을 알 수 있다.
우리는 그럼 명제자체가 아니라, 명제의 구성요소인 "모래더미"에 대해서 좀더 깊게 파고들어보자.
10억개의 모래입자로 구성된 모래더미가 있다고 가정했을떄, 우리는 3억개 미만의 모래입자를 가진 모래더미는 모래더미가 아니다! 라고 정의하자.
위의 좀 더 명확한 정의에 의해서 300,000,000의 모래입자를 가진 모래더미는 모래더미이다.
220px-Tannin_heap.jpeg
[Obejct 1]
이젠 299,999,999의 모래입자를 가진 "모래더미"가 아닌 "모래더미"를 살펴보자.
220px-Tannin_heap.jpeg
[Object 2]
Object 1과 Object 2는 전혀차이가 없다, 다만, Object 1은 모래더미이고 Object 2는 모래더미가 아닌 모래더미이다.
심각한 모순이 발생한다.
여기서 우리는 조금 더 조건을 확대해보기로 하자. 3억개나 한알 없는거나 별차이가 없으니, 3천개 미만부터는 모래더미가 아니라 가정하자.
Hanalei.JPG
2,999개의 모래알을 가진 모래"들"이다. 확실히 모래더미는 아니다. 이제는 완벽히 정의가 되었구나!
그런데 여기서 잠깐, 3,000개의 모래알을 가진 모래"들"은 모래더미인가?
당연하지, 애초에 우리가 정의를 그렇게 했잖아?
그런데 2,999개의 모래알을 가진 모래"들"과 3,000개의 모래알을 가진 "모래더미"는 전혀 차이가 없다.
또다시 모순이 발생한다.
download (1).jpg
논리식에는 전혀 잘못된 점이 없다. 과연 무엇이 잘못된 것일까?
우리는 모래"한 알"이라는 아주 정밀하고 미세한 오차가 '더미'라는 모호한 단위에 가려지면서 생기는 역설의 함정에 빠져버린 것이다.
그러나 중요한점은, 우리는 이 모호한 단위 '더미'를 정의하면 정의하려 들수록 또다른 모순을 낳게된다.
구체적으로 모래더미라 부를 수 있는 모래알의 갯수는 몇개인가? 그리고 그 모래알의 갯수보다 '단 한 알' 적은 모래더미를 모래더미가 아니라 할 수 있는가?
logic.jpg
이 장난같은 수수께끼를 해결하기위해, 이에대한 제대로된 논리와 오류를 논파하려고 무려 수천년간 수학자, 철학자, 논리학자들이 연구와 토론을 해왔으나
아직까지 이렇다할 대답은 나오지 않고있는 논리수학, 논리철학의 난제이다.
Sand-pile paradox (모래더미의 역설) 혹은 논리체계를 확장시켜 Sorites paradox (연쇄논법 역설) 이라고 부른다.
picture-48-1360100722.jpg
[Daniel Dennett (1942~) 하버드 대학교와 옥스포드 대학교 철학, 논리학과 출신의 논리학자]
이에 대해서 수학자들과 논리학자들은 의견이 분분한데, "애초에 그 더미라는건 상대적으로 존재하나, 절대적으로는 존재하지 않는것이다" 라고 주장하는 학자들도 있다.
그러나 또다시 논리를 수학적으로 확장시키면, 위 이론에서 또다시 "더미는 존재한다" 라는 일축된 논리를 이끌어 낼 수 있으므로 자가모순(Self-referential paradox)이기 때문에, 미국의 논리학자 Daniel Dennett은 "그렇게 생각하는건 위험한 짓이다" 라고 일축한다.
예를 들면, "어제 해가 떴고, 오늘도 해가 떴으므로, 내일도 해가 뜰것이다" 라는 논리는 타당한 논리이면서 동시에 타당하지 않은 논리이다.
왜냐하면 그 논리체계 내에서는 어떠한 오류도 가지지 않는다. 그러나 이 논리체계 밖으로 벗어나서 "해" 라는 객체 자체만을 바라보자면
"해"는 78억년후 적색거성에서 원시성거성으로 변하며 폭발, 사망한다.
sun-clouds-blue-sky-14641020076aM.jpg
그럼 "내일도 해가 뜰것" 이라는 명제는 78억년 전까지는 확고한 논리이다. 즉, P(n)에 대하여 n에 관한 Domain(정의역)을 정확히 정의해야만 비로소
논리가 확고해 지는 것이다. 그러나 논리체계 안에서의 시스템 만으로는 이 논리를 확고히 하는 것이 불가능하다. 왜냐하면 어제도 해가 떴고, 오늘도
해가 떴으니 내일은 해가 뜰것이라는 것을 우리는 "귀납적"으로 추론가능할뿐, 결코 해라는 존재의 수명 및 기타 정보에 대해서는 논리체계상으로는 알 수 없기 때문이다.
즉, 해라는 것은 논리체계 안에서가 아니라 논리체계 밖에서 연역적으로 분석되어야 한다.
그래야 비로소 우리는 "어제 해가 떴고, 오늘도 해가 떴으므로, 현세가 21세기 이므로, 대략 78억년 전까지 해는 내일 계속 뜰것이다" 라는 빈틈없는 논리를 성립시킬수 있다.
모래더미의 역설로 잠깐 넘어가서, 우리는 그렇다면 "모래더미"라는 존재의 단위를 구체적으로 해를 분석하듯이 연역적으로 분석할 필요가 있다.
과연 모래더미를 모래더미로 '파악'하게 만드는 것은 무엇인가? 모래더미를 이루는 요소(componenet)는 무엇인가?
그러나 해의 수명과는 다르게 모래더미에 대한 정확한 분석은 한마디로 "애매"하다.
Color_gradient_illustrating_a_sorites_paradox_with_labels.png
위의 그림을 살펴보자. Graphical color 상에서 초록색의 색상이 빨간색의 색상과 Gradient를 이루는 모습이다.
우리는 부분 부분을 큼직하게 자르면 그 부분들의 색깔을 비교적 정확하게 정의할 수 있고, 이를 구분할 수 있다. (Distinguishable)
그러나 이 부분 부분을 아주 미세하고 많은 조각으로 "무수히 많이" 구분하면, 우리는 바로 옆칸의 색깔과 그 옆칸의 색깔의 차이를 구분할 수 없다. (Indistinguishable)
바로 이 때문에, 모래더미에서의 모래알과 같은 위에서 보듯 미세한 조각과 모래알 하나가 빠진 모래더미의 차이를 전혀 구분할 수 없는것이다.
즉, 우리는 이 모래더미 문제를 Indistinguishable case로 놔두어야하는 운명일지도 모른다. 초록색을 초록색으로 구분짓는 '개념' 모래더미를 모래더미로 구분짓는 모래알의 갯수에 대한 '개념'이 너무나 애매모호하기 때문이다.
deltaeps.gif
[Epsilon-Delta definition of limit]
수학적으로 '극한'에 대해서도 (ε, δ definition of limit) 엡실론-델타 극한 정의를 통한 정확한 정의가 이루어져야만 비로소 극한을 이해할 수 있다.
이를 통해서 수학자들과 비수학자들간에 상당히 많은 의견차이가 보여지는 그 유명한 0.99999... = 1 이라는 명제도 "한없이 가까워진다" 라는 정의가 너무나 애매하기 때문에 발생되는 것이다.
PRhVb.png
또한, 밀레니엄 문제의 하나인 P-NP 문제도 이러한 "일정규모라 정의된 일정규모에서 하나의 구성요소가 빠져도 그 해답을 그대로 유지해야한다"라는 수학적 귀납법의 논리가 불완전하기에 발생하는 문제이다.
쉽게 검산가능한 문제는 쉽게 풀리는가? 라는 단순한 문제에서, 쉽게 검산가능한 문제들의 집합 중 P = {x l x = 쉽게풀리는 문제들의 집합} NP = {x l x = 적어도
검산은 쉽게풀리지만 문제는 불확실한 문제들의 집합} 인데,
여기서 P집합이 NP의 subset인가 아닌가에 대한 문제인데, 이는 귀납적으로 모래더미의 역설에서 보여진 수학적 귀납법이 가지는 오류를 정확히 정의하고 파악할 수 없기때문에 생기는 난제이다.
모래더미를 모래더미로 파악하게 만드는 정확한 요소에 대한 "정의"는 아직까지도 미궁에 빠져있다. (그것이 모래알의 갯수가 되었건 부피이건 무엇이되었건)
이에 대해 시대를 풍미했던 오스트리아의 천재 철학자, 논리학자 Ludwig Wittgenstein (루트비히 비트겐슈타인)은 이런 유명한 말을 남긴다.
download (2).jpg
[Ludwig Wittgenstein 1889 Vienna, Austria - 1951 Cambridge, United Kingdom]
- "개념이란 애매한 개념이다" (정의란 애매한 정의이다) -
우리는 일상에서 이와같은 애매한 개념과 함께 맞닥뜨리는 논리적 모순을 "최대한"으로 피하기 위하여 정확하고 엄밀한 정의를 하려 노력한다.
그러나, 그 엄밀하게 정의된 무언가에서 하나의 오류가 발생한다면, 우리는 그 엄밀한 정의와 논리 밖에서 그 오류점을 찾아내야한다.
이는 상당히 심오하고 수학적, 철학적인 접근으로, 수학의 위상수학, 군론과 집합론에서 다루는 개념들에 대한 상당한 연구와 지식, 그리고 철학적 배경이 동원된다.
그리고 그 오류를 마침내 발견했다면, 우리는 그 오류를 간파하고 역설이 존재할 수 없는 또다른 논리체계, 공리체계를 만들기도 하는데,
그렇게 수학과 논리학, 철학은 모두 Reductionism 에 의해서 발전한다. (i.e Russell's Axioms or Axiom of Reducibility)
결국 우리는, 모래더미가 "구체적으로 어떠한 조건을 가질때 모래더미가 되며, 그 구체적인 조건의 개념과 정의가 무엇인가"를 끊임없이 고민하고 살아가야하는 것이다.
무수히 많은 모래들이 이루는 고요함과 더불어 사막에서만 찾아볼 수 있는 진귀한 풍경들도 많다. 특히, 미국 동,남부~중부에 걸쳐있는 광활한 Desert valley의 모래들은 상당히 부드럽고 입자가 무척작다.
그럼 여기서 모래더미를 잠깐 살펴보자.
487610394.jpg
어릴때 늘 모래를 가지고 놀았듯이, 우리는 위의 "모래더미"에서 모래알 하나씩을 뺴내고 그릇에 옮기는 놀이를 해보기로 하자.
우리는 모래알 한알을 빼내어 그릇에 옮겨놓았다.
이 모래알 한알이 빠진 "모래더미"는 여전히 "모래더미"이다.
이번엔 두번째, 세번째 시도를 해보자.
...
몇알이 빠졌던 상관없이 "모래더미"는 여전히 건재하다. 왜냐하면 몇알이 빠졌던 상관없이 "모래더미"는 여전히 모래더미이기 때문이다.
그런데 셀수없이 많은 시도를 해보자면 모래더미는 결국 모래알 한알만 남게될 것이다.
그러나 앞선 논리에 따르자면 이 모래알 한알만 남은 모래더미 "조차도" 훌륭한 [모래더미]가 된다.
depositphotos_11060156-stock-photo-3d-white-leaning-back-against.jpg
뭔가 이상하다. 분명 우리는 한번, 두번, 세번 ... 시도를 해도 눈앞에 모래더미가 여전히 남아있다는 사실을 이해할 수 있다.
그러나 계속 시도를 하게되면 남아있는 그 "모래더미"는 결국 "모래더미"가 아니게 된다.
우리는 상황이 조금더 복잡하고 심각해진다는것을 예감할 수 있다.
조금더 수학적, 논리적으로 접근을 해보자.
1. 모래더미는 모래들의 집합이다
2. 모래더미에서 n개 정도의 모래알을 덜어낸다고 해서 기존의 모래더미와의 차이가 크지 않으므로, n+1개의 모래알을 덜어내도 여전히 모래더미이다.
3. 1) 2)의 논리와 수학적 귀납법 (Mathematical Induction)을 이용하면 모래를 모두 덜어내어도 여전히 모래더미이다.
220px-Tannin_heap.jpeg
아니다. 우리는 2번까지는 고개를 끄덕이며 동의하지만, 3번의 논리에는 고개를 완강히 저으며 "당연히 아니다" 라고 말할 수 있다.
그러나 1,2,3번의 논리에는 어떠한 논리적 오류도 존재하지 않는다.
여기서 수학적 귀납법이 뭘까? 다음과 같은 연역법(Deductive reasoning)의 한 방법이다.
51-induction-5-638.jpg
1. 어떠한 Proposition (명제) P(n)에 관해서 P(1) 혹은 P(0)과 같은 "자명한" 경우에 명제가 성립함을 밝힌다
2. P(n)이 P(k)일때 성립한다고 가정한뒤, P(n) = P(k+1)임을 증명한다.
3. k=1일때 P(n)이 성립한다면, P(k+1)일때도 성립해야하므로, P(2)일때도 성립, 이를 반복, k에 대하여 P(n)이 무한히 성립한다.
조금더 쉽게 풀어쓰자면
1. 첫번째 도미노가 쓰러지는지 확인한다
2. n번째 도미노가 쓰러지면 n+1 번째 도미노도 쓰러진다는 것을 확인한다
3. 결국 모든 도미노는 무사히 쓰러진다
결국 수학적 귀납법에 의해서 명제 P(n) = "n개의 모래알을 뺀 모래더미는 여전히 모래더미다" 의 도미노는 모두 무사히 쓰러져야"한다".
그런데, 우리는 그렇지 않다는것을 알 수 있다.
우리는 그럼 명제자체가 아니라, 명제의 구성요소인 "모래더미"에 대해서 좀더 깊게 파고들어보자.
10억개의 모래입자로 구성된 모래더미가 있다고 가정했을떄, 우리는 3억개 미만의 모래입자를 가진 모래더미는 모래더미가 아니다! 라고 정의하자.
위의 좀 더 명확한 정의에 의해서 300,000,000의 모래입자를 가진 모래더미는 모래더미이다.
220px-Tannin_heap.jpeg
[Obejct 1]
이젠 299,999,999의 모래입자를 가진 "모래더미"가 아닌 "모래더미"를 살펴보자.
220px-Tannin_heap.jpeg
[Object 2]
Object 1과 Object 2는 전혀차이가 없다, 다만, Object 1은 모래더미이고 Object 2는 모래더미가 아닌 모래더미이다.
심각한 모순이 발생한다.
여기서 우리는 조금 더 조건을 확대해보기로 하자. 3억개나 한알 없는거나 별차이가 없으니, 3천개 미만부터는 모래더미가 아니라 가정하자.
Hanalei.JPG
2,999개의 모래알을 가진 모래"들"이다. 확실히 모래더미는 아니다. 이제는 완벽히 정의가 되었구나!
그런데 여기서 잠깐, 3,000개의 모래알을 가진 모래"들"은 모래더미인가?
당연하지, 애초에 우리가 정의를 그렇게 했잖아?
그런데 2,999개의 모래알을 가진 모래"들"과 3,000개의 모래알을 가진 "모래더미"는 전혀 차이가 없다.
또다시 모순이 발생한다.
download (1).jpg
논리식에는 전혀 잘못된 점이 없다. 과연 무엇이 잘못된 것일까?
우리는 모래"한 알"이라는 아주 정밀하고 미세한 오차가 '더미'라는 모호한 단위에 가려지면서 생기는 역설의 함정에 빠져버린 것이다.
그러나 중요한점은, 우리는 이 모호한 단위 '더미'를 정의하면 정의하려 들수록 또다른 모순을 낳게된다.
구체적으로 모래더미라 부를 수 있는 모래알의 갯수는 몇개인가? 그리고 그 모래알의 갯수보다 '단 한 알' 적은 모래더미를 모래더미가 아니라 할 수 있는가?
logic.jpg
이 장난같은 수수께끼를 해결하기위해, 이에대한 제대로된 논리와 오류를 논파하려고 무려 수천년간 수학자, 철학자, 논리학자들이 연구와 토론을 해왔으나
아직까지 이렇다할 대답은 나오지 않고있는 논리수학, 논리철학의 난제이다.
Sand-pile paradox (모래더미의 역설) 혹은 논리체계를 확장시켜 Sorites paradox (연쇄논법 역설) 이라고 부른다.
picture-48-1360100722.jpg
[Daniel Dennett (1942~) 하버드 대학교와 옥스포드 대학교 철학, 논리학과 출신의 논리학자]
이에 대해서 수학자들과 논리학자들은 의견이 분분한데, "애초에 그 더미라는건 상대적으로 존재하나, 절대적으로는 존재하지 않는것이다" 라고 주장하는 학자들도 있다.
그러나 또다시 논리를 수학적으로 확장시키면, 위 이론에서 또다시 "더미는 존재한다" 라는 일축된 논리를 이끌어 낼 수 있으므로 자가모순(Self-referential paradox)이기 때문에, 미국의 논리학자 Daniel Dennett은 "그렇게 생각하는건 위험한 짓이다" 라고 일축한다.
예를 들면, "어제 해가 떴고, 오늘도 해가 떴으므로, 내일도 해가 뜰것이다" 라는 논리는 타당한 논리이면서 동시에 타당하지 않은 논리이다.
왜냐하면 그 논리체계 내에서는 어떠한 오류도 가지지 않는다. 그러나 이 논리체계 밖으로 벗어나서 "해" 라는 객체 자체만을 바라보자면
"해"는 78억년후 적색거성에서 원시성거성으로 변하며 폭발, 사망한다.
sun-clouds-blue-sky-14641020076aM.jpg
그럼 "내일도 해가 뜰것" 이라는 명제는 78억년 전까지는 확고한 논리이다. 즉, P(n)에 대하여 n에 관한 Domain(정의역)을 정확히 정의해야만 비로소
논리가 확고해 지는 것이다. 그러나 논리체계 안에서의 시스템 만으로는 이 논리를 확고히 하는 것이 불가능하다. 왜냐하면 어제도 해가 떴고, 오늘도
해가 떴으니 내일은 해가 뜰것이라는 것을 우리는 "귀납적"으로 추론가능할뿐, 결코 해라는 존재의 수명 및 기타 정보에 대해서는 논리체계상으로는 알 수 없기 때문이다.
즉, 해라는 것은 논리체계 안에서가 아니라 논리체계 밖에서 연역적으로 분석되어야 한다.
그래야 비로소 우리는 "어제 해가 떴고, 오늘도 해가 떴으므로, 현세가 21세기 이므로, 대략 78억년 전까지 해는 내일 계속 뜰것이다" 라는 빈틈없는 논리를 성립시킬수 있다.
모래더미의 역설로 잠깐 넘어가서, 우리는 그렇다면 "모래더미"라는 존재의 단위를 구체적으로 해를 분석하듯이 연역적으로 분석할 필요가 있다.
과연 모래더미를 모래더미로 '파악'하게 만드는 것은 무엇인가? 모래더미를 이루는 요소(componenet)는 무엇인가?
그러나 해의 수명과는 다르게 모래더미에 대한 정확한 분석은 한마디로 "애매"하다.
Color_gradient_illustrating_a_sorites_paradox_with_labels.png
위의 그림을 살펴보자. Graphical color 상에서 초록색의 색상이 빨간색의 색상과 Gradient를 이루는 모습이다.
우리는 부분 부분을 큼직하게 자르면 그 부분들의 색깔을 비교적 정확하게 정의할 수 있고, 이를 구분할 수 있다. (Distinguishable)
그러나 이 부분 부분을 아주 미세하고 많은 조각으로 "무수히 많이" 구분하면, 우리는 바로 옆칸의 색깔과 그 옆칸의 색깔의 차이를 구분할 수 없다. (Indistinguishable)
바로 이 때문에, 모래더미에서의 모래알과 같은 위에서 보듯 미세한 조각과 모래알 하나가 빠진 모래더미의 차이를 전혀 구분할 수 없는것이다.
즉, 우리는 이 모래더미 문제를 Indistinguishable case로 놔두어야하는 운명일지도 모른다. 초록색을 초록색으로 구분짓는 '개념' 모래더미를 모래더미로 구분짓는 모래알의 갯수에 대한 '개념'이 너무나 애매모호하기 때문이다.
deltaeps.gif
[Epsilon-Delta definition of limit]
수학적으로 '극한'에 대해서도 (ε, δ definition of limit) 엡실론-델타 극한 정의를 통한 정확한 정의가 이루어져야만 비로소 극한을 이해할 수 있다.
이를 통해서 수학자들과 비수학자들간에 상당히 많은 의견차이가 보여지는 그 유명한 0.99999... = 1 이라는 명제도 "한없이 가까워진다" 라는 정의가 너무나 애매하기 때문에 발생되는 것이다.
PRhVb.png
또한, 밀레니엄 문제의 하나인 P-NP 문제도 이러한 "일정규모라 정의된 일정규모에서 하나의 구성요소가 빠져도 그 해답을 그대로 유지해야한다"라는 수학적 귀납법의 논리가 불완전하기에 발생하는 문제이다.
쉽게 검산가능한 문제는 쉽게 풀리는가? 라는 단순한 문제에서, 쉽게 검산가능한 문제들의 집합 중 P = {x l x = 쉽게풀리는 문제들의 집합} NP = {x l x = 적어도
검산은 쉽게풀리지만 문제는 불확실한 문제들의 집합} 인데,
여기서 P집합이 NP의 subset인가 아닌가에 대한 문제인데, 이는 귀납적으로 모래더미의 역설에서 보여진 수학적 귀납법이 가지는 오류를 정확히 정의하고 파악할 수 없기때문에 생기는 난제이다.
모래더미를 모래더미로 파악하게 만드는 정확한 요소에 대한 "정의"는 아직까지도 미궁에 빠져있다. (그것이 모래알의 갯수가 되었건 부피이건 무엇이되었건)
이에 대해 시대를 풍미했던 오스트리아의 천재 철학자, 논리학자 Ludwig Wittgenstein (루트비히 비트겐슈타인)은 이런 유명한 말을 남긴다.
download (2).jpg
[Ludwig Wittgenstein 1889 Vienna, Austria - 1951 Cambridge, United Kingdom]
- "개념이란 애매한 개념이다" (정의란 애매한 정의이다) -
우리는 일상에서 이와같은 애매한 개념과 함께 맞닥뜨리는 논리적 모순을 "최대한"으로 피하기 위하여 정확하고 엄밀한 정의를 하려 노력한다.
그러나, 그 엄밀하게 정의된 무언가에서 하나의 오류가 발생한다면, 우리는 그 엄밀한 정의와 논리 밖에서 그 오류점을 찾아내야한다.
이는 상당히 심오하고 수학적, 철학적인 접근으로, 수학의 위상수학, 군론과 집합론에서 다루는 개념들에 대한 상당한 연구와 지식, 그리고 철학적 배경이 동원된다.
그리고 그 오류를 마침내 발견했다면, 우리는 그 오류를 간파하고 역설이 존재할 수 없는 또다른 논리체계, 공리체계를 만들기도 하는데,
그렇게 수학과 논리학, 철학은 모두 Reductionism 에 의해서 발전한다. (i.e Russell's Axioms or Axiom of Reducibility)
결국 우리는, 모래더미가 "구체적으로 어떠한 조건을 가질때 모래더미가 되며, 그 구체적인 조건의 개념과 정의가 무엇인가"를 끊임없이 고민하고 살아가야하는 것이다.
빠르게 두꺼운 팔 근육 만들기 위한 방법.
이번에 쓰는 글은 빠르게 두꺼운 팔 근육 만들기 위한 방법에 관한 것임.
굽은어깨를 쓸 때도 그랬지만 웨이트 트레이닝 입문자를 위해
쉽고 간결하게 쓰기 때문에 내용이 부실 해 보일수도 있다.
웨이트 트레이닝 고수들은 괜히 보다가 싸움만 날게 뻔해서
안보는 것을 추천한다.
일단 웨이트 트레이닝 입문자라서 주 3회 운동이 어려울 수도 있어서
주 2회 하는 것을 권한다
운동해야 할 부위는 가장먼저 4부위다.
어느 한 가지라도 빠트린다면 결국 나중에 다시 채워야 되니
운동할 때 빠트리지 않고 하는게 중요하다.
관련 이미지
그림에 보면 뒷팔 즉 삼두근 그리고 앞에 있는 이두근
그리고 빨갛게 색칠된 부분에 상완요골근
마지막으로
전완근에 대한 이미지 검색결과
전완근이다.
운동도 당연히 4가지를 해야 하는데
내가 소개하는 운동 방법은 내가 팔운동 하면서 내 신체에 맞는 운동이고
지금도 계속 하고 있는 운동이다.
내 신체와 다르다면 안맞을 수도 있기 때문에 자신의 신체에 맞지 않다면
다른 운동을 하는 것을 추천한다
스트레이트 바 즉 일직선으로 된 바가 자신의 체형에 맞지 않다면
이지바에 대한 이미지 검색결과
이지 바 라고 구부러진 모양의 바가 있으니 이 걸로 하면 됨.
이지바도 안맞는다면 덤벨로 해라.
윗팔, 즉 이두 부분을 단련하기 위한 운동 방법인데 덤벨 컬 이라고 한다.
바벨 컬이나 구부러진 바를 이용해 할 수도 있지만
웨이트 트레이닝 입문자들은 근력이 부족해 치팅이라고 몸을 이용해서 하는 경우가 있어서
덤벨로 하는 것을 추천한다.
또 덤벨로 하면 손목을 자유롭게 움직일 수 있어서 바를 이용할 때 생기는 부상을 피할 수 있음
영상에는 서서하는데 앉아서 하면 자세를 치팅 없이 엄격하게 수행할 수가 있어서
앉아서 하는게 좋다.
다음은 콘센트레이션 컬이라고
이두근의 단부 부분과 상완근을 동원해서 이두근을 보다 둥근 형태로 만들어 주는 운동임.
상완근을 굵게 만들면 이두근이 위로 밀려나서 봉우리를 돋보이게 할 수 있다
우람한 근육을 만드는데 좋은 방법은 아닌데
일반 컬보다 상완근을 좀더 많이 동원해서
균형있는 팔로 만들어 준다.
주 2회 운동을 한다면 한번은 덤벨 컬 한번은 콘센트레이션 컬을 하는 것도 좋음.
다음 운동은 상완요골근인데 키우기 쉬운 근육이다.
hammer curl에 대한 이미지 검색결과
해머컬이라고 상완근도 개입을 하는 운동임.
위에 있는 콘센트레이션 컬이 힘들다면 해머컬로 대체 해도 된다.
내 신체를 기준으로 해머컬은 상완근 보다는
상완 요골근이 더 많이 개입을 함 비율로 따지자면 상완근 3 상완 요골근 7 정도.
동작도 매우 쉬운 편이라 입문자들도 보면 바로 따라할 수 있다.
세번째로 전완 운동인데
wrist curl에 대한 이미지 검색결과
리스트 컬 이라고 전완의 안쪽 부분을 단련해주는 운동임.
wrist extension에 대한 이미지 검색결과
이건 리스트 익스텐션 이라고
전완의 바깥 부분을 단련하는 운동이다.
보통 해머컬을 하고 나면 전완의 힘도 별로 안남아 있어서
저중량으로 하는 것을 추천한다.
어차피 운동 좀 하다보면 해머컬 하고나서도 힘이 많이 남고
또 전완을 단련하기에 아주 좋은 운동임.
이것도 덤벨 컬과 마찬가지로
주 2회 운동을 하니깐
월요일 날 리버스 컬을 했다면
목요일 날은 리스트 컬을 하는게 좋다
괜히 리버스 컬 4셋트 하고 또 리스트 컬 4셋 한다면
몸만 상하는 지름길임.
마지막 운동으로
관련 이미지
삼두근인데
사실 삼두근 운동은 어려운 편에 속한다.
감각을 느끼기도 어렵고 또 한국인은 팔 다리가 짧아서
삼두근이 짧은 사람이 많다.
게다가 이름 그대로 세가지의 두 외측두,장두,내측두로 구성되있고
각 부분별로 불균형이 아주 흔하게 일어나서 내부가 발달하면
외부는 지체되고 외부가 발달하면 내부가 지체된다.
또 체형에 따라 운동 방법이 많이 달라지기 때문에
내가 여기서 어떤 것이 가장 좋다! 라고 말할 수도 없음.
그래서 내가 하는 운동을 소개 할텐데
이 방법은 입문자들에게는 다소 어려울 수도 있으니
조심하는게 좋다.
트라이셉스 익스텐션이라 하는데
위 동영상은 이지 바를 이용한 운동이고
아래는 덤벨을 이용하는거임
나는 워밍업으로 덤벨을 이용해서 2셋트 정도 하고
스트레이트 일직선으로 된 걸로 운동을 한다.
이 트라이셉스 익스텐션이 내 체형에 가장 잘 맞았다.
입문자들에게 추천하는 운동은
kick back에 대한 이미지 검색결과
킥 백 인데 삼두근 고립운동임.
삼두근을 단련하는 운동 중에 가장 쉬운 동작인데
신장이 거의 일어나지 않아서 감각을 잘 못느끼는 사람도 있을거야.
하지만 내가 하는 트라이셉스 익스텐션이나 딥스는 입문자가 하기엔 좀
힘들지.
그래서 킥백을 추천한다.
그리고 일단 팔을 키울려면
비싼 쇠 아령을 살건지 아니면 비교적 싼 pvc 조립 덤벨을 살건지 선택 해야 함.
chrome dumbbell에 대한 이미지 검색결과
이런 크롬 도금 아령을 무게별로 맞추는 것도 돈 많이 나감.
chrome dumbbell에 대한 이미지 검색결과
관련 이미지
이런 것도 있는데 이것도 역시 비싼 편임.
관련 이미지
이걸 pvc 조립덤벨이라고 하는데 가격이 싸다.
그게 장점임
단점으로는 무게가 올라가면 올라갈수록 크롬이나 주물에 비해 넓어지고 두꺼워짐.
근데 나는 해머컬을 할 때 pvc 조립 덤벨로 해머컬을 한다
그 이유는 크롬은 무게가 높아도 옆으로 넓지 않아서 상완요골근에
집중하기 좀 어려운데 pvc는 무게가 높으면 옆으로 넓어서
상완 요골근에 집중하기가 쉬워짐.
그래서 나는 해머컬을 할 때 조립 덤벨로 한다.
일단 돈이 없으면 pvc로 가는게 좋다.
그리고 가장 중요한 것은
rubber dumbbell에 대한 이미지 검색결과
고무덤벨은 절대 사지마라.
고무냄새 엄청나게 나고 엄청 빠지지도 않는다
나도 입문할 때 싸다고 고무덤벨을 샀는데
냄새가 너무 심해서 마당에 놨고
2년이 지난 지금도 냄새가 나더라
입문자를 위해 팔 근육 빨리 키우는 방법에 대해 글을 써 봤는데
운동은 진짜로 사람마다 체형이 달라서 어느 방법이 좋고
스트레이트 바가 좋거나 덤벨이 좋거나 이지바가 좋거나라고 확실히
말을 할 수도 없다.
4가지 부위를 써 놨는데
입문자들은 저 4가지를 하는 것이 아마 힘들거야
그래서 덤벨 컬하고 킥백만 하다가
다른 운동도 추가하는 것도 나쁘지 않다.
굽은어깨를 쓸 때도 그랬지만 웨이트 트레이닝 입문자를 위해
쉽고 간결하게 쓰기 때문에 내용이 부실 해 보일수도 있다.
웨이트 트레이닝 고수들은 괜히 보다가 싸움만 날게 뻔해서
안보는 것을 추천한다.
일단 웨이트 트레이닝 입문자라서 주 3회 운동이 어려울 수도 있어서
주 2회 하는 것을 권한다
운동해야 할 부위는 가장먼저 4부위다.
어느 한 가지라도 빠트린다면 결국 나중에 다시 채워야 되니
운동할 때 빠트리지 않고 하는게 중요하다.
관련 이미지
그림에 보면 뒷팔 즉 삼두근 그리고 앞에 있는 이두근
그리고 빨갛게 색칠된 부분에 상완요골근
마지막으로
전완근에 대한 이미지 검색결과
전완근이다.
운동도 당연히 4가지를 해야 하는데
내가 소개하는 운동 방법은 내가 팔운동 하면서 내 신체에 맞는 운동이고
지금도 계속 하고 있는 운동이다.
내 신체와 다르다면 안맞을 수도 있기 때문에 자신의 신체에 맞지 않다면
다른 운동을 하는 것을 추천한다
스트레이트 바 즉 일직선으로 된 바가 자신의 체형에 맞지 않다면
이지바에 대한 이미지 검색결과
이지 바 라고 구부러진 모양의 바가 있으니 이 걸로 하면 됨.
이지바도 안맞는다면 덤벨로 해라.
윗팔, 즉 이두 부분을 단련하기 위한 운동 방법인데 덤벨 컬 이라고 한다.
바벨 컬이나 구부러진 바를 이용해 할 수도 있지만
웨이트 트레이닝 입문자들은 근력이 부족해 치팅이라고 몸을 이용해서 하는 경우가 있어서
덤벨로 하는 것을 추천한다.
또 덤벨로 하면 손목을 자유롭게 움직일 수 있어서 바를 이용할 때 생기는 부상을 피할 수 있음
영상에는 서서하는데 앉아서 하면 자세를 치팅 없이 엄격하게 수행할 수가 있어서
앉아서 하는게 좋다.
다음은 콘센트레이션 컬이라고
이두근의 단부 부분과 상완근을 동원해서 이두근을 보다 둥근 형태로 만들어 주는 운동임.
상완근을 굵게 만들면 이두근이 위로 밀려나서 봉우리를 돋보이게 할 수 있다
우람한 근육을 만드는데 좋은 방법은 아닌데
일반 컬보다 상완근을 좀더 많이 동원해서
균형있는 팔로 만들어 준다.
주 2회 운동을 한다면 한번은 덤벨 컬 한번은 콘센트레이션 컬을 하는 것도 좋음.
다음 운동은 상완요골근인데 키우기 쉬운 근육이다.
hammer curl에 대한 이미지 검색결과
해머컬이라고 상완근도 개입을 하는 운동임.
위에 있는 콘센트레이션 컬이 힘들다면 해머컬로 대체 해도 된다.
내 신체를 기준으로 해머컬은 상완근 보다는
상완 요골근이 더 많이 개입을 함 비율로 따지자면 상완근 3 상완 요골근 7 정도.
동작도 매우 쉬운 편이라 입문자들도 보면 바로 따라할 수 있다.
세번째로 전완 운동인데
wrist curl에 대한 이미지 검색결과
리스트 컬 이라고 전완의 안쪽 부분을 단련해주는 운동임.
wrist extension에 대한 이미지 검색결과
이건 리스트 익스텐션 이라고
전완의 바깥 부분을 단련하는 운동이다.
보통 해머컬을 하고 나면 전완의 힘도 별로 안남아 있어서
저중량으로 하는 것을 추천한다.
어차피 운동 좀 하다보면 해머컬 하고나서도 힘이 많이 남고
또 전완을 단련하기에 아주 좋은 운동임.
이것도 덤벨 컬과 마찬가지로
주 2회 운동을 하니깐
월요일 날 리버스 컬을 했다면
목요일 날은 리스트 컬을 하는게 좋다
괜히 리버스 컬 4셋트 하고 또 리스트 컬 4셋 한다면
몸만 상하는 지름길임.
마지막 운동으로
관련 이미지
삼두근인데
사실 삼두근 운동은 어려운 편에 속한다.
감각을 느끼기도 어렵고 또 한국인은 팔 다리가 짧아서
삼두근이 짧은 사람이 많다.
게다가 이름 그대로 세가지의 두 외측두,장두,내측두로 구성되있고
각 부분별로 불균형이 아주 흔하게 일어나서 내부가 발달하면
외부는 지체되고 외부가 발달하면 내부가 지체된다.
또 체형에 따라 운동 방법이 많이 달라지기 때문에
내가 여기서 어떤 것이 가장 좋다! 라고 말할 수도 없음.
그래서 내가 하는 운동을 소개 할텐데
이 방법은 입문자들에게는 다소 어려울 수도 있으니
조심하는게 좋다.
트라이셉스 익스텐션이라 하는데
위 동영상은 이지 바를 이용한 운동이고
아래는 덤벨을 이용하는거임
나는 워밍업으로 덤벨을 이용해서 2셋트 정도 하고
스트레이트 일직선으로 된 걸로 운동을 한다.
이 트라이셉스 익스텐션이 내 체형에 가장 잘 맞았다.
입문자들에게 추천하는 운동은
kick back에 대한 이미지 검색결과
킥 백 인데 삼두근 고립운동임.
삼두근을 단련하는 운동 중에 가장 쉬운 동작인데
신장이 거의 일어나지 않아서 감각을 잘 못느끼는 사람도 있을거야.
하지만 내가 하는 트라이셉스 익스텐션이나 딥스는 입문자가 하기엔 좀
힘들지.
그래서 킥백을 추천한다.
그리고 일단 팔을 키울려면
비싼 쇠 아령을 살건지 아니면 비교적 싼 pvc 조립 덤벨을 살건지 선택 해야 함.
chrome dumbbell에 대한 이미지 검색결과
이런 크롬 도금 아령을 무게별로 맞추는 것도 돈 많이 나감.
chrome dumbbell에 대한 이미지 검색결과
관련 이미지
이런 것도 있는데 이것도 역시 비싼 편임.
관련 이미지
이걸 pvc 조립덤벨이라고 하는데 가격이 싸다.
그게 장점임
단점으로는 무게가 올라가면 올라갈수록 크롬이나 주물에 비해 넓어지고 두꺼워짐.
근데 나는 해머컬을 할 때 pvc 조립 덤벨로 해머컬을 한다
그 이유는 크롬은 무게가 높아도 옆으로 넓지 않아서 상완요골근에
집중하기 좀 어려운데 pvc는 무게가 높으면 옆으로 넓어서
상완 요골근에 집중하기가 쉬워짐.
그래서 나는 해머컬을 할 때 조립 덤벨로 한다.
일단 돈이 없으면 pvc로 가는게 좋다.
그리고 가장 중요한 것은
rubber dumbbell에 대한 이미지 검색결과
고무덤벨은 절대 사지마라.
고무냄새 엄청나게 나고 엄청 빠지지도 않는다
나도 입문할 때 싸다고 고무덤벨을 샀는데
냄새가 너무 심해서 마당에 놨고
2년이 지난 지금도 냄새가 나더라
입문자를 위해 팔 근육 빨리 키우는 방법에 대해 글을 써 봤는데
운동은 진짜로 사람마다 체형이 달라서 어느 방법이 좋고
스트레이트 바가 좋거나 덤벨이 좋거나 이지바가 좋거나라고 확실히
말을 할 수도 없다.
4가지 부위를 써 놨는데
입문자들은 저 4가지를 하는 것이 아마 힘들거야
그래서 덤벨 컬하고 킥백만 하다가
다른 운동도 추가하는 것도 나쁘지 않다.
수 체계(Numeral system)의 역사
일상생활에서 우리는 무수히 많은 '수'와 마주하고 산다.
그게 어떠한 형태이든 형태가 없는 것이던, '수'는 인류의 삶과 함께해왔다.
태초의 인류는 멧돼지 '두'마리, 사과 '한'개 등과 같이 셀 수 있는 수에만 집중해왔다.
그러나 의식주가 해결되고나서 부터는 무언가 다른 점들이 인간에게 생각을 시키기 시작하였다.
"옆 마을에서 사과 100개를 선물로 주었는데 우리가 가진 사과는 200개이다. 우리는 몇개의 사과를 가지고 있는가?"
download.jpeg
100개에서 200개를 더가지고있다, 인류는 "더" 가지게 되었다의 의미를 생각하게된다.
100 (더 가지게되다) 200 = 300.
인류는 100보만큼의 거리에서 200보만큼을 더 걸었을때, 결국엔 300보를 걸은것이 된다는 사실을 자연적으로 인지하게된다. 그리고, 300보에서 다시 10개 만큼을 먹었을때, 10보만큼을 뒤로 후진하게되면 290보를 걸은것이 된다는 사실을 인지한다.
여기서 "더하기" 와 "빼기" 라는 대수학의 태초가 시작된다.
_-Logo.gif
그런데 여기서 한 똘똘한 사람이 한 가지 재밌는 사실을 깨닫는다.
"작년에도 사과 100개를 선물받았고, 올해에도 사과 100개를 선물받았으니 사과 100개를 "두 번" 받은것이되네?"
두 번, 세 번, 네 번.. 이 몇번째의 의미는 무엇일까?
인류는 이번의 문제는 단순히 걸음걸이 보만으로는 해결할 수 없을것같다는 느낌을 받는다. 100개가 "두번" 있으면 200개이다. 만약 100개를 몇번받았는데 그게 200개라면, 그건 "두번" 받은 것이다.
인류는 '정의'를 내리기 시작한다.
download (1).jpeg
이후 수천년간 빙하기를 거치며 인류는 세상의 모든 진리를 습득했다고 생각한다.
그런데 고대의 인도에서 이 태초의 사칙연산에 누군가 의문을 품는다.
"만약 10에서 10을 빼면 이것도 수인가?"
여기서 아주 기이하고 신비로운 숫자 "0"이 탄생한다.
그러나, 아주 신비로우면서도 감미로운 이 새로운 발견들에, 인류의 호기심은 끝나지 않는다.
10에서 11을 빼면 그것도 수인가? 아무것도 없는 것보다 더 작을 수 있는가? 아무것도 없는 것에서 아무것도 없는 번만큼 곱하면 어떻게되나?
여기서 인류의 대수학을 폭발적으로 발전시킬 어떤 발명가가 등장한다
quote-to-avoide-the-tediouse-repetition-of-these-woordes-is-equalle-to-i-will-settle-as-i-robert-recorde-90-86-06.jpg
[Robert Recorde 1510 Uk - 1558 Welsh Physician]
"무의미한 반복적인 말들을 생략하기 위해, 두개의 평행선(=)을 "~와 같다"라는 기호로 "정의"한다."
Robert Recorde는 +, -를 비롯한 사칙연산의 기호와 =의 부호를 수학에 도입함으로써 인류의 "사과 100개가 있었는데 옆마을에서 200개를 받으면 300개를 가진게 된다" 에서 "100 + 200 = 300", "100 x 2 = 200", "200 ÷ 2 = 100" "300-10 = 290" 으로 아주 간단한 연산체계를 가지게만든다.
인류는 최단시간에 자신의 의문점을 아주 간단한 수식으로 쓸 수 있게된다.
여기서부터 시작되는 대수학적 의문
10 - 11 = ?
5 ÷ 3 = ?
그러나 이는 이미 기원전의 그리스의 한 수학자가 이미 결론지은 문제였다.
69947310f656b6b8cef27038809d07a6792f04da874fe707e488b34940c8b2ee37fe2aa3521f69015c4bbf9cfd80a23ff90592ff07a03ede416c985696bf3f482bca274eaf5c19e546a6f3da251189ec.jpeg
[Pythagoras BC 570 - BC 490]
"모든 수는 분수(fraction)라는 수체계로써 표현가능하다"
피타고라스는 모든 수체계는 3/5, 4/7과 같이 분수체계로 정의될 수 있다고 믿었다. 그리고 유클리드의 기하원론에서 확장하여 직각삼각형 세변을 이용한 획기적인 공식을 발견한다.
'... It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.'
'... 직각삼각형의 직각의 대변의 길이의 제곱은 나머지 두 변의 길이의 제곱의 합과 같다."
고대 그리스에서 발견된 "수학적 진리". 피타고라스는 모든 수는 결국 이 직각삼각형의 변에 대입되면 분수의 꼴로 나타날 수 밖에는 없다라고 믿었다.
그러나 불행하게도, 피타고라스 자신의 진리는 자신의 진리를 깨부숴버리는 또다른 진리를 낳는다.
real-numbers-5-638.jpg
[Hippasus BC 500 - ?]
"직각의 대변이 아닌 두변이 각각 같은 직각삼각형의 대변의 길이는 분수인가?"
피타고라스 학파의 일원이었던 Hippasus는 두변의 길이가 같은 직각삼각형의 대변은 지금까지 존재하던 피타고라스의 유리수 체계에는 존재하지 않는다는 것을 알게된다.
"√2를 무리수가 아닌 유리수라 가정하고, √2 = p/q로 놓는다. 이 때 p와 q는 서로소이다. 양변을 제곱하여 p² = 2q²로 만든다. p²은 짝수이므로 p도 짝수이다 (p²=2q²이므로). p = 2k로 놓고, 위의 식에 대입한다. 4k² = 2q² 이므로, 2k² = q² 이다. 그러므로 q 역시 짝수이다. p와 q가 모두 짝수면 서로소가 아니므로 가정에 모순된다."
만약 값이 분수라면, 분수꼴로 변형될 수 있어야한다.
이를 분수꼴로 나타내면, 이는 결국 무한히 통분되는 분수를 낳게된다.
이는 지금껏 보아왔던 피타고라스의 유리수와는 전혀다른 체계의 수이다.
이를 "무리수"는 피타고라스에게 납득될 수 없던 진리였기에 결국 히파수스를 암살하였다고 전해진다. (혹은 히파수스를 제물로 바쳤다고도 전해진다)
1280px-Bronnikov_gimnpifagoreizev.jpg
[Pythagoreanism 피타고라스 학파 -Fyodor Bronnikov]
이런 역사를 가진 무리수는 대수학을 폭발적으로 발전시킨다.
대수학적 공리계 안에서 존재하는 수많은 함수들이 발전되면서, 무리수는 각별한 관심을 받게된다.
그러나 인류의 호기심은 여기서 끝이 아니었다.
16세기 프랑스의 한 시골에서, 근대철학과 근대수학의 문을 연 한 경이로운 천재가 등장한다
f4d900893274a0e74b47661b030cc4cb7c8250c43f59880bc3d73acbe1f0ed7adecd25a7757ead9e1b752fbe1204545d7783a44c613345e55203613f64f78cc3bc9f8120c1977bc4004d2869a8386c3f.jpeg
[René Descartes 1596 - 1650]
"2차방정식 x^2 = (-1)의 해를 만족시키는 값은 존재하는가"
image11.gif
이차함수(Quadratic function) x^2 = f(x) 에서 vertex point (0,0) 밑으로는 어떠한 함수값도 존재하지 않는다.
그러나, 존재하지 않는것이 존재하는가?
몸이 불편해서 늘 침대에 누워지냈던 데카르트는 직선으로 이루어진 천장의 파리의 구체적인 위치를 나타낼 수 있는 방법을 생각하다가, 직교좌표계(Coordinate plane)를 생각해낸다.
곧, 수많은 다항고차함수(Polynomial function)들이 직교좌표에 그려지게 된다. 그러나 데카르트에게있어 2차함수에서 한가지 의문을 낳는점은 밑으로 존재하지않는 함수값은 존재하지 않는가였다.
이 아이디어를 이어받아, 데카르트의 시대에 활동하던 또다른 스위스의 천재수학자가 등장한다.
Leonhard_Euler.jpg
[Leonhard euler 1707 - 1783 "the father of mathematical analysis"]
이차함수 x^2 = f(x)의 vertex point밑으로 존재하지 않는 함수값이 존재한다고 "정의"하자.
그리고 이를 허수값 i (i^2 = -1)라 부르기로 "정의"한다.
이로써, 집합론의 유리수 집합[Q] 밖의 또다른 수체계 허수[I]가 등장한다. 수학자들은 이를 복소수 체계[C]라 부르기로 정의한다.
이로써 해석학, 컴퓨터공학, 근대물리학은 폭발적으로 발전하기 시작한다.
시간은 상대적으로 계의 속도에 따라 다른 물리변화량이다.
로렌츠 요소(Lorentz factor), 1/√(1-v^2/c^2)) 에 의거한 아인슈타인은 "계의 속도가 빛의 속도를 넘어서는순간, 시간은 허수값을 가지며 흐른다"는 특수 상대성 이론을 정립하는 등, 물리학, 해석학 등은 엄청난 발전을 한다.
Albert_Einstein_Head.jpg
[Albert Einstein 1879 - 1955]
복소수의 발전은 대수학 뿐만 아니라 모든 분야에서 많은 산물을 낳았다. 복소수체계로 인한 3그래픽과 컴퓨터공학 및 암호학은 매우 근대적으로 발전했다.
그런데, 인간의 호기심은 아직도 끝나지 않았다.
19세기 영국 글래스고에서 한 물리수학자가 등장한다.
sir-william-rowan-hamilton-4.jpg
[Sir William Hamilton, 9th Baronet 1788-1856]
'복소수[C] 밖의 3차원공간에서 환[Ring 대수학의 구조]을 이루는 수체계는 존재하는가'
허수단위와 똑같이, 해밀턴은 j와 k 값을 생각하기 시작한다.
'i^2 = -1 j^2 = -1 k^2 = -1, ijk = -1 , i ≠ j ≠ k 가정하자, 이는 3차원 환을 이루는가'
해밀턴에 의해 복소수 밖의 외계적 수체계가 등장한다. 이를 사원수(Quaternion)이라 정의하고, [H]라 부르기로 정의한다.
e5e35f071a4d75e0c56b8a68bd81bd8f4706d576.png
해석기하학적으로 설명하자면, 허수체계는 2차원에서 평면의 회전을 담당하지만, 해밀턴의 사원수는 "3차원" 공간에서의 회전을 담당한다.
이로써 3차원 공간의 유체역학이 발달하기 시작한다.
라이트형제로 인해서 발전된 비행기는, 해밀턴의 사원수와 함께 비행이 정밀하게 공학적으로 발전되어 결국 오늘날의 "항공기"로 발전한다.
F18.png
[해밀턴의 사원수 공간(Hamilton Quaternion plane)에서의 항공기의 분석]
WhRCV3n.gif
대수적으로 수학자들은 이제 수체계를 "정의"를 내리고 확장하고 싶어한다
즉, 수체계 적으로 사원수 공간이 존재하고 팔원수 공간도 (결합법칙 성립x, 4차원공간) 존재하고 16원수 공간(교환법칙 성립x, 5차원 공간) ... 도 존재한다.
과연 저것들이 어디에쓰일까? 라고 생각할 수 있겠지만, 놀랍게도 팔원수는 양자영학에서 친숙하게 쓰이며, 해밀턴의 사원수는 3차원 공간의 컴퓨터 그래픽 발전을 이끔으로써 일본, 미국의 애니메이션 발전에 거대한 공로를 이루었다.
결합법칙, 교환법칙이 성립하지 않는 8, 16원수 들은 일반적인 대수적 수로써는 쓰이지 않는다. 이는 어떤 문제를 해결하기 위한 알고리즘 도구 정도로 쓰이는 수체계라고 볼수도 있다. (2^n 에 해당하는 수들은 모두 2^ n원수를 가진다) 다만, 현재까지 수학자들이 끊임없이 낳고있는 궁금증은, 과연 3^n , 5^n 에 해당하는 원수 체계는 환을 이루지 않는가에 대한 것이며, 이원수 체계가 존재한다면 0원수 체계도 존재하는가, 혹은 그 원수체계 자체 밖의 수체계도 존재하는가이다.
82fdc21eaf9a1c38744835bfe77d5172.jpg
인류의 역사는 겨우 30만년이 되지 않는다. 지구 역사의 0.000001% 정도의 부분조차도 차지하지 않는 짧은 역사이다.
이 기간에 인류가 사과 100개에서 200개를 더하는 것을 계산하는 것부터, 해석학의 발전, 대수학의 발전과 해밀턴 사원수 공간을 이용한 항공기, 그래픽, 컴퓨터의 발전까지 이 모든것은 수학이 함께해왔다.
그러나 현재까지 인간이 밝혀낸 수학적 진리는 전체의 겨우 10%도 되지않는다. 아니, 어쩌면 10% 정도라도 밝혀냈다고 말하는것은 너무나 과장된 발언일 것이다.
0.1%의 조차도 제대로 밝혀내지 못하고 무수한 수학은 라 불리는 베일에 감싸져있다.
중요한점은, 이 모든 수학이 인류의 호기심이 발전시킨 산물이며, 수억개의 은하단과 수억개의 은하수, 수억개의 별들과 수억개의 행성들 사이에서 조그만 생물로 태어난 인간이 가진 "최고"의 유산이라는 것이다.
gamma-function.png
[Riemann Gamma function Γ(n) = (n−1)!]
그게 어떠한 형태이든 형태가 없는 것이던, '수'는 인류의 삶과 함께해왔다.
태초의 인류는 멧돼지 '두'마리, 사과 '한'개 등과 같이 셀 수 있는 수에만 집중해왔다.
그러나 의식주가 해결되고나서 부터는 무언가 다른 점들이 인간에게 생각을 시키기 시작하였다.
"옆 마을에서 사과 100개를 선물로 주었는데 우리가 가진 사과는 200개이다. 우리는 몇개의 사과를 가지고 있는가?"
download.jpeg
100개에서 200개를 더가지고있다, 인류는 "더" 가지게 되었다의 의미를 생각하게된다.
100 (더 가지게되다) 200 = 300.
인류는 100보만큼의 거리에서 200보만큼을 더 걸었을때, 결국엔 300보를 걸은것이 된다는 사실을 자연적으로 인지하게된다. 그리고, 300보에서 다시 10개 만큼을 먹었을때, 10보만큼을 뒤로 후진하게되면 290보를 걸은것이 된다는 사실을 인지한다.
여기서 "더하기" 와 "빼기" 라는 대수학의 태초가 시작된다.
_-Logo.gif
그런데 여기서 한 똘똘한 사람이 한 가지 재밌는 사실을 깨닫는다.
"작년에도 사과 100개를 선물받았고, 올해에도 사과 100개를 선물받았으니 사과 100개를 "두 번" 받은것이되네?"
두 번, 세 번, 네 번.. 이 몇번째의 의미는 무엇일까?
인류는 이번의 문제는 단순히 걸음걸이 보만으로는 해결할 수 없을것같다는 느낌을 받는다. 100개가 "두번" 있으면 200개이다. 만약 100개를 몇번받았는데 그게 200개라면, 그건 "두번" 받은 것이다.
인류는 '정의'를 내리기 시작한다.
download (1).jpeg
이후 수천년간 빙하기를 거치며 인류는 세상의 모든 진리를 습득했다고 생각한다.
그런데 고대의 인도에서 이 태초의 사칙연산에 누군가 의문을 품는다.
"만약 10에서 10을 빼면 이것도 수인가?"
여기서 아주 기이하고 신비로운 숫자 "0"이 탄생한다.
그러나, 아주 신비로우면서도 감미로운 이 새로운 발견들에, 인류의 호기심은 끝나지 않는다.
10에서 11을 빼면 그것도 수인가? 아무것도 없는 것보다 더 작을 수 있는가? 아무것도 없는 것에서 아무것도 없는 번만큼 곱하면 어떻게되나?
여기서 인류의 대수학을 폭발적으로 발전시킬 어떤 발명가가 등장한다
quote-to-avoide-the-tediouse-repetition-of-these-woordes-is-equalle-to-i-will-settle-as-i-robert-recorde-90-86-06.jpg
[Robert Recorde 1510 Uk - 1558 Welsh Physician]
"무의미한 반복적인 말들을 생략하기 위해, 두개의 평행선(=)을 "~와 같다"라는 기호로 "정의"한다."
Robert Recorde는 +, -를 비롯한 사칙연산의 기호와 =의 부호를 수학에 도입함으로써 인류의 "사과 100개가 있었는데 옆마을에서 200개를 받으면 300개를 가진게 된다" 에서 "100 + 200 = 300", "100 x 2 = 200", "200 ÷ 2 = 100" "300-10 = 290" 으로 아주 간단한 연산체계를 가지게만든다.
인류는 최단시간에 자신의 의문점을 아주 간단한 수식으로 쓸 수 있게된다.
여기서부터 시작되는 대수학적 의문
10 - 11 = ?
5 ÷ 3 = ?
그러나 이는 이미 기원전의 그리스의 한 수학자가 이미 결론지은 문제였다.
69947310f656b6b8cef27038809d07a6792f04da874fe707e488b34940c8b2ee37fe2aa3521f69015c4bbf9cfd80a23ff90592ff07a03ede416c985696bf3f482bca274eaf5c19e546a6f3da251189ec.jpeg
[Pythagoras BC 570 - BC 490]
"모든 수는 분수(fraction)라는 수체계로써 표현가능하다"
피타고라스는 모든 수체계는 3/5, 4/7과 같이 분수체계로 정의될 수 있다고 믿었다. 그리고 유클리드의 기하원론에서 확장하여 직각삼각형 세변을 이용한 획기적인 공식을 발견한다.
'... It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.'
'... 직각삼각형의 직각의 대변의 길이의 제곱은 나머지 두 변의 길이의 제곱의 합과 같다."
고대 그리스에서 발견된 "수학적 진리". 피타고라스는 모든 수는 결국 이 직각삼각형의 변에 대입되면 분수의 꼴로 나타날 수 밖에는 없다라고 믿었다.
그러나 불행하게도, 피타고라스 자신의 진리는 자신의 진리를 깨부숴버리는 또다른 진리를 낳는다.
real-numbers-5-638.jpg
[Hippasus BC 500 - ?]
"직각의 대변이 아닌 두변이 각각 같은 직각삼각형의 대변의 길이는 분수인가?"
피타고라스 학파의 일원이었던 Hippasus는 두변의 길이가 같은 직각삼각형의 대변은 지금까지 존재하던 피타고라스의 유리수 체계에는 존재하지 않는다는 것을 알게된다.
"√2를 무리수가 아닌 유리수라 가정하고, √2 = p/q로 놓는다. 이 때 p와 q는 서로소이다. 양변을 제곱하여 p² = 2q²로 만든다. p²은 짝수이므로 p도 짝수이다 (p²=2q²이므로). p = 2k로 놓고, 위의 식에 대입한다. 4k² = 2q² 이므로, 2k² = q² 이다. 그러므로 q 역시 짝수이다. p와 q가 모두 짝수면 서로소가 아니므로 가정에 모순된다."
만약 값이 분수라면, 분수꼴로 변형될 수 있어야한다.
이를 분수꼴로 나타내면, 이는 결국 무한히 통분되는 분수를 낳게된다.
이는 지금껏 보아왔던 피타고라스의 유리수와는 전혀다른 체계의 수이다.
이를 "무리수"는 피타고라스에게 납득될 수 없던 진리였기에 결국 히파수스를 암살하였다고 전해진다. (혹은 히파수스를 제물로 바쳤다고도 전해진다)
1280px-Bronnikov_gimnpifagoreizev.jpg
[Pythagoreanism 피타고라스 학파 -Fyodor Bronnikov]
이런 역사를 가진 무리수는 대수학을 폭발적으로 발전시킨다.
대수학적 공리계 안에서 존재하는 수많은 함수들이 발전되면서, 무리수는 각별한 관심을 받게된다.
그러나 인류의 호기심은 여기서 끝이 아니었다.
16세기 프랑스의 한 시골에서, 근대철학과 근대수학의 문을 연 한 경이로운 천재가 등장한다
f4d900893274a0e74b47661b030cc4cb7c8250c43f59880bc3d73acbe1f0ed7adecd25a7757ead9e1b752fbe1204545d7783a44c613345e55203613f64f78cc3bc9f8120c1977bc4004d2869a8386c3f.jpeg
[René Descartes 1596 - 1650]
"2차방정식 x^2 = (-1)의 해를 만족시키는 값은 존재하는가"
image11.gif
이차함수(Quadratic function) x^2 = f(x) 에서 vertex point (0,0) 밑으로는 어떠한 함수값도 존재하지 않는다.
그러나, 존재하지 않는것이 존재하는가?
몸이 불편해서 늘 침대에 누워지냈던 데카르트는 직선으로 이루어진 천장의 파리의 구체적인 위치를 나타낼 수 있는 방법을 생각하다가, 직교좌표계(Coordinate plane)를 생각해낸다.
곧, 수많은 다항고차함수(Polynomial function)들이 직교좌표에 그려지게 된다. 그러나 데카르트에게있어 2차함수에서 한가지 의문을 낳는점은 밑으로 존재하지않는 함수값은 존재하지 않는가였다.
이 아이디어를 이어받아, 데카르트의 시대에 활동하던 또다른 스위스의 천재수학자가 등장한다.
Leonhard_Euler.jpg
[Leonhard euler 1707 - 1783 "the father of mathematical analysis"]
이차함수 x^2 = f(x)의 vertex point밑으로 존재하지 않는 함수값이 존재한다고 "정의"하자.
그리고 이를 허수값 i (i^2 = -1)라 부르기로 "정의"한다.
이로써, 집합론의 유리수 집합[Q] 밖의 또다른 수체계 허수[I]가 등장한다. 수학자들은 이를 복소수 체계[C]라 부르기로 정의한다.
이로써 해석학, 컴퓨터공학, 근대물리학은 폭발적으로 발전하기 시작한다.
시간은 상대적으로 계의 속도에 따라 다른 물리변화량이다.
로렌츠 요소(Lorentz factor), 1/√(1-v^2/c^2)) 에 의거한 아인슈타인은 "계의 속도가 빛의 속도를 넘어서는순간, 시간은 허수값을 가지며 흐른다"는 특수 상대성 이론을 정립하는 등, 물리학, 해석학 등은 엄청난 발전을 한다.
Albert_Einstein_Head.jpg
[Albert Einstein 1879 - 1955]
복소수의 발전은 대수학 뿐만 아니라 모든 분야에서 많은 산물을 낳았다. 복소수체계로 인한 3그래픽과 컴퓨터공학 및 암호학은 매우 근대적으로 발전했다.
그런데, 인간의 호기심은 아직도 끝나지 않았다.
19세기 영국 글래스고에서 한 물리수학자가 등장한다.
sir-william-rowan-hamilton-4.jpg
[Sir William Hamilton, 9th Baronet 1788-1856]
'복소수[C] 밖의 3차원공간에서 환[Ring 대수학의 구조]을 이루는 수체계는 존재하는가'
허수단위와 똑같이, 해밀턴은 j와 k 값을 생각하기 시작한다.
'i^2 = -1 j^2 = -1 k^2 = -1, ijk = -1 , i ≠ j ≠ k 가정하자, 이는 3차원 환을 이루는가'
해밀턴에 의해 복소수 밖의 외계적 수체계가 등장한다. 이를 사원수(Quaternion)이라 정의하고, [H]라 부르기로 정의한다.
e5e35f071a4d75e0c56b8a68bd81bd8f4706d576.png
해석기하학적으로 설명하자면, 허수체계는 2차원에서 평면의 회전을 담당하지만, 해밀턴의 사원수는 "3차원" 공간에서의 회전을 담당한다.
이로써 3차원 공간의 유체역학이 발달하기 시작한다.
라이트형제로 인해서 발전된 비행기는, 해밀턴의 사원수와 함께 비행이 정밀하게 공학적으로 발전되어 결국 오늘날의 "항공기"로 발전한다.
F18.png
[해밀턴의 사원수 공간(Hamilton Quaternion plane)에서의 항공기의 분석]
WhRCV3n.gif
대수적으로 수학자들은 이제 수체계를 "정의"를 내리고 확장하고 싶어한다
즉, 수체계 적으로 사원수 공간이 존재하고 팔원수 공간도 (결합법칙 성립x, 4차원공간) 존재하고 16원수 공간(교환법칙 성립x, 5차원 공간) ... 도 존재한다.
과연 저것들이 어디에쓰일까? 라고 생각할 수 있겠지만, 놀랍게도 팔원수는 양자영학에서 친숙하게 쓰이며, 해밀턴의 사원수는 3차원 공간의 컴퓨터 그래픽 발전을 이끔으로써 일본, 미국의 애니메이션 발전에 거대한 공로를 이루었다.
결합법칙, 교환법칙이 성립하지 않는 8, 16원수 들은 일반적인 대수적 수로써는 쓰이지 않는다. 이는 어떤 문제를 해결하기 위한 알고리즘 도구 정도로 쓰이는 수체계라고 볼수도 있다. (2^n 에 해당하는 수들은 모두 2^ n원수를 가진다) 다만, 현재까지 수학자들이 끊임없이 낳고있는 궁금증은, 과연 3^n , 5^n 에 해당하는 원수 체계는 환을 이루지 않는가에 대한 것이며, 이원수 체계가 존재한다면 0원수 체계도 존재하는가, 혹은 그 원수체계 자체 밖의 수체계도 존재하는가이다.
82fdc21eaf9a1c38744835bfe77d5172.jpg
인류의 역사는 겨우 30만년이 되지 않는다. 지구 역사의 0.000001% 정도의 부분조차도 차지하지 않는 짧은 역사이다.
이 기간에 인류가 사과 100개에서 200개를 더하는 것을 계산하는 것부터, 해석학의 발전, 대수학의 발전과 해밀턴 사원수 공간을 이용한 항공기, 그래픽, 컴퓨터의 발전까지 이 모든것은 수학이 함께해왔다.
그러나 현재까지 인간이 밝혀낸 수학적 진리는 전체의 겨우 10%도 되지않는다. 아니, 어쩌면 10% 정도라도 밝혀냈다고 말하는것은 너무나 과장된 발언일 것이다.
0.1%의 조차도 제대로 밝혀내지 못하고 무수한 수학은 라 불리는 베일에 감싸져있다.
중요한점은, 이 모든 수학이 인류의 호기심이 발전시킨 산물이며, 수억개의 은하단과 수억개의 은하수, 수억개의 별들과 수억개의 행성들 사이에서 조그만 생물로 태어난 인간이 가진 "최고"의 유산이라는 것이다.
gamma-function.png
[Riemann Gamma function Γ(n) = (n−1)!]
2017년 10월 15일 일요일
지난달에 유튜브로 57달러 범
57달러면 송금환율 고려하면
1100원 X 57 = 6.2만원 정도 된다.
뭐 별로 대단한거 한거 없으면서도 이정도 돈이 벌렸다는거에 대해서 기분이 좋기도 하고생각보다 많이 벌리지 않는다는 것에 약간 우울해지기도 하고 그렇다
암튼 내가 유튜브를 시작할 때 1view 당 1원의 ㅣ수입이 발생한다는 루머를 들었었는데,
그건 진짜 말그대로 루머 아니 거짓말이고,
1뷰당 평균 0.1원 정도의 수입도 나올까 말까다.
아마 구독자가 많고 영상 길이가 길어서 중간광고도 몇개씩 삽입될 수 있는 크리에이터들에게는 1뷰당 0.5원까지 나올지 모르겠지만 일반 유튜버들에게는 1뷰당 0.1원이 맞는것 같다.
그러니깐 유튜브 광고로만 먹고산다는 생각보다는 이 크리에이터로 유명해져서 외부광고와 수입을 늘릴 수 있는 방법을 생각해봐야 하겠다고 생각했다..
하지만 영상을 전공하지도 영상관련 지식도 전무한 나같은 사람들에게는 킬러콘텐츠가 있어서 가끔 용돈이 들어오는 수준으로 생각해야지 이걸 전업으로 생각하려면 좀 늦은 감이 없지 않다,.
개인적인 유튜브 운영 한달 수입 57달러의 소회였습니다. 다음달에는 200달러 그 다음에는 400 또 800 1600 3200 6400 기하급수적으로 늘어났으면 좋겠네요
1100원 X 57 = 6.2만원 정도 된다.
뭐 별로 대단한거 한거 없으면서도 이정도 돈이 벌렸다는거에 대해서 기분이 좋기도 하고생각보다 많이 벌리지 않는다는 것에 약간 우울해지기도 하고 그렇다
암튼 내가 유튜브를 시작할 때 1view 당 1원의 ㅣ수입이 발생한다는 루머를 들었었는데,
그건 진짜 말그대로 루머 아니 거짓말이고,
1뷰당 평균 0.1원 정도의 수입도 나올까 말까다.
아마 구독자가 많고 영상 길이가 길어서 중간광고도 몇개씩 삽입될 수 있는 크리에이터들에게는 1뷰당 0.5원까지 나올지 모르겠지만 일반 유튜버들에게는 1뷰당 0.1원이 맞는것 같다.
그러니깐 유튜브 광고로만 먹고산다는 생각보다는 이 크리에이터로 유명해져서 외부광고와 수입을 늘릴 수 있는 방법을 생각해봐야 하겠다고 생각했다..
하지만 영상을 전공하지도 영상관련 지식도 전무한 나같은 사람들에게는 킬러콘텐츠가 있어서 가끔 용돈이 들어오는 수준으로 생각해야지 이걸 전업으로 생각하려면 좀 늦은 감이 없지 않다,.
개인적인 유튜브 운영 한달 수입 57달러의 소회였습니다. 다음달에는 200달러 그 다음에는 400 또 800 1600 3200 6400 기하급수적으로 늘어났으면 좋겠네요
2017년 10월 10일 화요일
2017년 9월 16일 토요일
2017년 5월 23일 화요일
한국 아르헨티나 전반 하이라이트 이승우 골 백승호 페널티골 2:0
한국 미쳤다.
이건 4강 신화 재현이 아니라
우승까지 해도 무리 없을 실력과 전력이다.
최강이라 불리는 아르헨티나를 2:0으로 가볍게 바르고 시작하는 전반전
이승우의 메시 빙의 골은 압권 중 압권이고
조영욱이 얻은 페널티킥을 엄청 침착하게 마무리 하는 백승호의 실력 역시
명불허전.
이거 이러다가 우승하는거 아니냐
이건 4강 신화 재현이 아니라
우승까지 해도 무리 없을 실력과 전력이다.
최강이라 불리는 아르헨티나를 2:0으로 가볍게 바르고 시작하는 전반전
이승우의 메시 빙의 골은 압권 중 압권이고
조영욱이 얻은 페널티킥을 엄청 침착하게 마무리 하는 백승호의 실력 역시
명불허전.
이거 이러다가 우승하는거 아니냐
2017년 3월 26일 일요일
스타크래프트1 리마스터 패키지 출시 2017년 여름 초읽기
드디어 스타1이 리마스터 된다고 합니다. 그래픽적으로 현실을 반영하여 4K UHD급 화질로 태세전환.
대세를 따라간다고 하는데, 스1 프로게이머들이 클로즈테스트에 참가하여 게임을 평가하니 그래픽이 너무 좋아 다른 게임같다고 평가를 했습니다.
다만, 드라군 에러등등 자잘한 게임 상 오류들은 그냥 스타1 그대로 두었고, 그래픽과 온라인배넷 사용을 더 활성화 했을 뿐이라고 합니다.
그럼에도 완전 무료로 게임을 즐길 수 있다고 하니 스타1을 좋아했던 분들이라면 한번 나올 때 구해서 플레이 해보는 것도 좋을 것 같습니다.
대세를 따라간다고 하는데, 스1 프로게이머들이 클로즈테스트에 참가하여 게임을 평가하니 그래픽이 너무 좋아 다른 게임같다고 평가를 했습니다.
다만, 드라군 에러등등 자잘한 게임 상 오류들은 그냥 스타1 그대로 두었고, 그래픽과 온라인배넷 사용을 더 활성화 했을 뿐이라고 합니다.
그럼에도 완전 무료로 게임을 즐길 수 있다고 하니 스타1을 좋아했던 분들이라면 한번 나올 때 구해서 플레이 해보는 것도 좋을 것 같습니다.
2017년 1월 10일 화요일
블로그스팟 네이버 웹마스터도구 등록하기 [rss/sitemap]
역시 갓 구글.
rss등록은 다들 되지만
sitemap까지 원샷으로 등록이 가능하다.
웹마스터도구에서
본인 구글스팟 주소 / feeds/posts/default?alt=rss
입력하고 rss등록요청하면 되고.
사이트맵 요청 페이지에서는
sitemap.xml
입력하면 끝.
역시 갓글 갓이버.
구글블로그가 네이버에 노출이 잡히면
모바일 통검 최적화는 아니지만 유입이 풍성해질 수 있음.
rss등록은 다들 되지만
sitemap까지 원샷으로 등록이 가능하다.
웹마스터도구에서
본인 구글스팟 주소 / feeds/posts/default?alt=rss
입력하고 rss등록요청하면 되고.
사이트맵 요청 페이지에서는
sitemap.xml
입력하면 끝.
역시 갓글 갓이버.
구글블로그가 네이버에 노출이 잡히면
모바일 통검 최적화는 아니지만 유입이 풍성해질 수 있음.
피드 구독하기:
덧글 (Atom)